| << problem 106 - Special subset sums: meta-testing |

|
Diophantine reciprocals I - problem 108 >> |
Problem 107: Minimal network
(see projecteuler.net/problem=107)
The following undirected network consists of seven vertices and twelve edges with a total weight of 243.
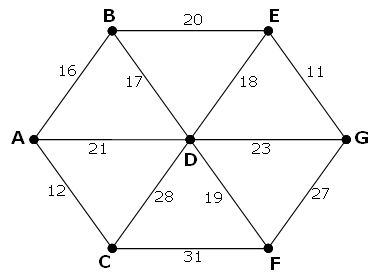
The same network can be represented by the matrix below.
ABCDEFG
A 161221
B16 1720
C12 28 31
D211728 181923
E 20 18 11
F 3119 27
G 231127
However, it is possible to optimise the network by removing some edges and still ensure that all points on the network remain connected.
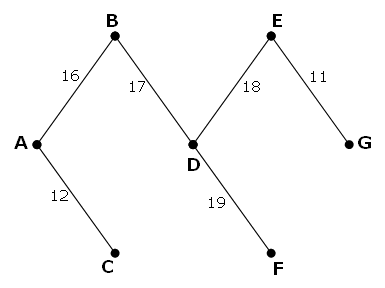
The network which achieves the maximum saving is shown below. It has a weight of 93, representing a saving of 243 - 93 = 150 from the original network.
Using network.txt (right click and 'Save Link/Target As...'), a 6K text file containing a network with forty vertices,
and given in matrix form, find the maximum saving which can be achieved by removing redundant edges whilst ensuring that the network remains connected.
My Algorithm
I use Prim's algorithm (see en.wikipedia.org/wiki/Prim's_algorithm):
donecontains these nodes where all connections are optimizeddonecontains initially an arbitrarily chosen node- algorithm is finished when
donecontains all nodes - in each iteration, one node is added to
done
- store all edges in
nextwhere one node is indoneand the other node isn't - sort
nextby the weight - pick the lowest
- add that edge to the optimized graph
minimal - add the other edge's node to
done, too
The "true" algorithm of Prim uses a priority queue quite efficiently whereas I rebuild it from scratch every time.
Nevertheless, my code solves the 2500x2500 networks of Hackerrank within less than a second.
Modifications by HackerRank
- the input format is completely different
- two nodes may be connected via multiple edges
- print the optimized weight instead of the gain
Interactive test
This feature is not available for the current problem.
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, as well as the input data, too. Or just jump to my GitHub repository.
The code contains #ifdefs to switch between the original problem and the Hackerrank version.
Enable #ifdef ORIGINAL to produce the result for the original problem (default setting for most problems).
//#define ORIGINAL
#include <iostream> #include <set> #include <map> #include <queue> typedef unsigned int Node; typedef unsigned int Weight; // connect two nodes and assign a weight
struct Edge { Node from; Node to; Weight weight; // for sorting bool operator<(const Edge& other) const { // STL's priority queue returns the __largest__ element first, therefore I invert the comparison sign if (weight != other.weight) return weight > other.weight; // sort by nodes, too, to avoid collisions of nodes with the same weight // the order doesn't matter, these nodes just "have to be different" if (from != other.from) return from < other.from; return to < other.to; } }; // all edges (full network)
std::map<std::pair<Node, Node>, Weight> network; // all nodes
std::set<Node> nodes; // weight of the full network, including duplicate connections
unsigned int initialSum = 0; // insert an edge into the network, true if already existing
void addEdge(Node from, Node to, Weight weight) { // count all originals weights initialSum += weight; // all edges have the lower ID first (I can do that because it's an undirected graph) if (from > to) std::swap(from, to); // already existing edge ? auto fromTo = std::make_pair(from, to); if (network.count(fromTo) != 0) // has the existing edge a lower or the same weight ? => we're done if (network[fromTo] <= weight) return; // store new (or improved) connection between two nodes network[fromTo] = weight; nodes.insert(from); nodes.insert(to); } int main() { #ifdef ORIGINAL // read Project Euler's weird file format for (unsigned int i = 0; i < 40; i++) for (unsigned int j = 0; j < 40; j++) { char c = 0; unsigned int weight = 0; // CSV-format while (c != ',' && c != '\n') { c = std::cin.get(); // ignore dashes if (c >= '0' && c <= '9') { weight *= 10; weight += c - '0'; } } // only valid weights if (weight != 0 && i < j) addEdge(i, j, weight); } #else // read Hackerrank input unsigned int numNodes, numEdges; std::cin >> numNodes >> numEdges; for (unsigned int i = 0; i < numEdges; i++) { Node from, to; Weight weight; std::cin >> from >> to >> weight; addEdge(from, to, weight); } #endif // optimized graph, initially empty std::set<Edge> minimal; // start with a random node std::set<Node> done; done.insert(*nodes.begin()); // not all nodes optimized yet ? while (done.size() < nodes.size()) { // add all edges where one node is part of tree and the other isn't std::priority_queue<Edge> next; for (auto e : network) { auto fromTo = e.first; bool hasFrom = done.count(fromTo.first) != 0; bool hasTo = done.count(fromTo.second) != 0; if (hasFrom == hasTo) // both nodes are already optimized or both aren't ? continue; next.push({fromTo.first, fromTo.second, e.second}); } // get edge with minimal weight auto add = next.top(); // add new edge to tree done.insert(add.from); // one insert is redundant but set::set throws it away done.insert(add.to); // add edge to the optimized graph minimal.insert(add); } // "measure" both graphs unsigned int optimizedSum = 0; for (auto i : minimal) optimizedSum += i.weight; #ifdef ORIGINAL // difference auto gain = initialSum - optimizedSum; std::cout << gain << std::endl; #else std::cout << optimizedSum << std::endl; #endif return 0; }
This solution contains 25 empty lines, 28 comments and 10 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in less than 0.01 seconds on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
May 11, 2017 submitted solution
May 11, 2017 added comments
Hackerrank
see https://www.hackerrank.com/contests/projecteuler/challenges/euler107
My code solves 8 out of 8 test cases (score: 100%)
Difficulty
Project Euler ranks this problem at 35% (out of 100%).
Hackerrank describes this problem as easy.
Note:
Hackerrank has strict execution time limits (typically 2 seconds for C++ code) and often a much wider input range than the original problem.
In my opinion, Hackerrank's modified problems are usually a lot harder to solve. As a rule thumb: brute-force is rarely an option.
Links
projecteuler.net/thread=107 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
C# www.mathblog.dk/project-euler-107-efficient-network/ (written by Kristian Edlund)
C# github.com/HaochenLiu/My-Project-Euler/blob/master/107.cs (written by Haochen Liu)
Python github.com/LaurentMazare/ProjectEuler/blob/master/e107.py (written by Laurent Mazare)
Python github.com/nayuki/Project-Euler-solutions/blob/master/python/p107.py (written by Nayuki)
Python github.com/steve98654/ProjectEuler/blob/master/107.py
C++ github.com/Meng-Gen/ProjectEuler/blob/master/107.cc (written by Meng-Gen Tsai)
C++ github.com/roosephu/project-euler/blob/master/107.cpp (written by Yuping Luo)
C++ github.com/steve98654/ProjectEuler/blob/master/107.cpp
C++ github.com/zmwangx/Project-Euler/blob/master/107/107.cpp (written by Zhiming Wang)
Java github.com/nayuki/Project-Euler-solutions/blob/master/java/p107.java (written by Nayuki)
Go github.com/frrad/project-euler/blob/master/golang/Problem107.go (written by Frederick Robinson)
Mathematica github.com/steve98654/ProjectEuler/blob/master/107.nb
Scala github.com/samskivert/euler-scala/blob/master/Euler107.scala (written by Michael Bayne)
Perl github.com/gustafe/projecteuler/blob/master/107-Minimal-network.pl (written by Gustaf Erikson)
Perl github.com/shlomif/project-euler/blob/master/project-euler/107/euler-107.pl (written by Shlomi Fish)
Rust github.com/gifnksm/ProjectEulerRust/blob/master/src/bin/p107.rs
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 106 - Special subset sums: meta-testing |

|
Diophantine reciprocals I - problem 108 >> |