| << problem 150 - Searching a triangular array for a sub-triangle ... |

|
Writing 1/2 as a sum of inverse squares - problem 152 >> |
Problem 151: Paper sheets of standard sizes: an expected-value problem
(see projecteuler.net/problem=151)
A printing shop runs 16 batches (jobs) every week and each batch requires a sheet of special colour-proofing paper of size A5.
Every Monday morning, the foreman opens a new envelope, containing a large sheet of the special paper with size A1.
He proceeds to cut it in half, thus getting two sheets of size A2. Then he cuts one of them in half to get two sheets of size A3
and so on until he obtains the A5-size sheet needed for the first batch of the week.
All the unused sheets are placed back in the envelope.
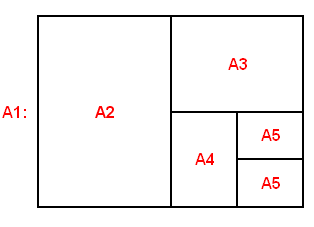
At the beginning of each subsequent batch, he takes from the envelope one sheet of paper at random.
If it is of size A5, he uses it. If it is larger, he repeats the 'cut-in-half' procedure until he has what he needs and any remaining sheets are always placed back in the envelope.
Excluding the first and last batch of the week, find the expected number of times (during each week) that the foreman finds a single sheet of paper in the envelope.
Give your answer rounded to six decimal places using the format x.xxxxxx .
My Algorithm
I solved this problem twice. My first attempt was running a Monte-Carlo simulation - and never achieved enough precision. That code is still present below.
My second (and successful) attempt evaluates the exact probabilities of each possible combination.
Its parameter is a simple container with 5 elements, where the first represents the number of A1 sheets, the second element stands for the number of A2 sheets, etc.
The initial parameter is { 1, 0, 0, 0, 0 }. If at some point we have no A5, no A4, 2x A3, no A4 and 1x A5 then it would be { 0, 0, 2, 0, 1 }.
Each sheet size is picked and the function calls itself recursively. The probability for picking a single sheet is 1 / numSheets.
If there are multiple sheets of the same sheet size i then the probability increases to sheets[i] / numSheets.
Interactive test
This feature is not available for the current problem.
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
#include <iostream> #include <vector> #include <iomanip> // return number of batch where a single sheet is in the envelope // parameter is a list of the number of available sheets, starting with A1 // e.g. 0x A5, 0x A4, 2x A3, 0x A4, 1x A5 is encoded as { 0, 0, 2, 0, 1 }
double evaluate(std::vector<unsigned int> sheets) { // count sheets unsigned int numSheets = 0; for (auto s : sheets) numSheets += s; // a single sheet ? double single = 0; if (numSheets == 1) { // only one sheet of A5 left => last batch if (sheets.back() == 1) return 0; // except if the single sheet is A1 (first batch) if (sheets.front() == 0) single = 1; } // process all sheet sizes for (size_t i = 0; i < sheets.size(); i++) { if (sheets[i] == 0) continue; auto next = sheets; // use one piece of the sheet size next[i]--; // cut it into smaller pieces for (size_t j = i + 1; j < next.size(); j++) next[j]++; // how likely do we pick this sheet size ? double probability = sheets[i] / (double)numSheets; // analyze next batch single += evaluate(next) * probability; } return single; } // I kept this code for historical reasons ... it's not called in main()
double montecarlo() { // more rounds improve precision const unsigned int NumRounds = 1000000; // different seeds yields different results ... srand(111); // how often a single sheet is observed unsigned int singleSheet = 0; for (unsigned int round = 0; round < NumRounds; round++) { // 1 => DIN A1, 2 => A2, ... 5 => A5 // this stack of sheets may contain some sizes multiple times const unsigned int SheetSizes = 5; unsigned int sheets[SheetSizes] = { 1,0,0,0,0 }; // one sheet A1 on Monday morning unsigned int numSheets = 1; // until all sheets are used (on Friday afternoon) while (numSheets > 0) { // a single sheet ? if (numSheets == 1) singleSheet++; // pick a random sheet unsigned int pick = rand() % numSheets; unsigned int current = 0; // select sheet size while (pick >= sheets[current]) pick -= sheets[current++]; // and remove one sheet sheets[current]--; // reduce total number of sheets, too numSheets--; // if the current sheet is larger than A5 then cut it into smaller sheets while (++current < SheetSizes) { sheets[current]++; numSheets++; } } // don't count the first and last batch (always one sheet) singleSheet -= 2; } return singleSheet / (double)NumRounds; } int main() { std::cout << std::fixed << std::setprecision(6); // start with one A1 sheet std::cout << evaluate({ 1,0,0,0,0 }) << std::endl; // my first approach was using a Monte-Carlo simulation but it converges too slowly //std::cout << montecarlo() << std::endl; return 0; }
This solution contains 19 empty lines, 29 comments and 3 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in 0.02 seconds on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
May 23, 2017 submitted solution
May 23, 2017 added comments
Difficulty
Project Euler ranks this problem at 35% (out of 100%).
Links
projecteuler.net/thread=151 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
Python github.com/nayuki/Project-Euler-solutions/blob/master/python/p151.py (written by Nayuki)
Python github.com/roosephu/project-euler/blob/master/151.py (written by Yuping Luo)
Python github.com/smacke/project-euler/blob/master/python/151.py (written by Stephen Macke)
Python github.com/steve98654/ProjectEuler/blob/master/151.py
C++ github.com/Meng-Gen/ProjectEuler/blob/master/151.cc (written by Meng-Gen Tsai)
C++ github.com/steve98654/ProjectEuler/blob/master/151.cpp
C github.com/LaurentMazare/ProjectEuler/blob/master/e151.c (written by Laurent Mazare)
Java github.com/HaochenLiu/My-Project-Euler/blob/master/151.java (written by Haochen Liu)
Java github.com/nayuki/Project-Euler-solutions/blob/master/java/p151.java (written by Nayuki)
Java github.com/thrap/project-euler/blob/master/src/Java/Problem151.java (written by Magnus Solheim Thrap)
Go github.com/frrad/project-euler/blob/master/golang/Problem151.go (written by Frederick Robinson)
Mathematica github.com/steve98654/ProjectEuler/blob/master/151.nb
Perl github.com/shlomif/project-euler/blob/master/project-euler/151/euler-151-v1.pl (written by Shlomi Fish)
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 150 - Searching a triangular array for a sub-triangle ... |

|
Writing 1/2 as a sum of inverse squares - problem 152 >> |