| << problem 207 - Integer partition equations |

|
Circular Logic - problem 209 >> |
Problem 208: Robot Walks
(see projecteuler.net/problem=208)
A robot moves in a series of one-fifth circular arcs (72°), with a free choice of a clockwise or an anticlockwise arc for each step, but no turning on the spot.
One of 70932 possible closed paths of 25 arcs starting northward is
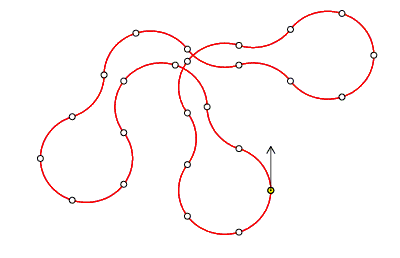
Given that the robot starts facing North, how many journeys of 70 arcs in length can it take that return it, after the final arc, to its starting position?
(Any arc may be traversed multiple times.)
My Algorithm
I played around with a 3rd party graphics library and tried to brute force the solution for 25 arcs:
- I set up rotation matrices
- need to adjust the allowed error to fix floating-point issues
- and had tons of other problems
More interesting is that I analyzed all paths with 5,6,7,...,25 arcs (obviously you need at least 5 arcs; I didn't analyze longer paths):
- there are only solutions for 5,10,15,20 and 25 arcs, that means the path length must be a multiple of 5
- the number of arcs "leaning left" is always a multiple of 5
- the number of arcs "leaning right" is always a multiple of 5
For example: 25 arcs means I have 5 full circles, some clockwise and some anti-clockwise, and these parts of the circle are connected in a "random" way.
The fascinating result of these observations: I don't need matrices at all - all I need is "counting" arcs !
- the path always starts with arc 0
- in each step I increment a counter in
numVisited[currentArc] - if the path turns left then I continue with the next arc (current arc plus 1 in modulo 5 → arc 1)
- if the path turns right then I continue with the previous arc (current arc minus 1 in modulo 5 → arc -1 → arc 4)
The whole state consists of these five counters plus the current arc.
I can merge these numbers into a single integer
id and store it in a container cache.Whenever I finish a path, all counters must have the same value.
If the first four value are identical then the fifth must be, too.
Instead of comparing the first four counters one-by-one I compare the first and second, the third and fourth and then the first and third.
This way I save one comparison (it's somehow like binary search):
"slow":
numVisited[0] == numVisited[1] && numVisited[1] == numVisited[2] && numVisited[2] == numVisited[3] && numVisited[3] == numVisited[4]"fast":
numVisited[0] == numVisited[1] && numVisited[3] == numVisited[4] && numVisited[1] == numVisited[3]→ actually my code does the opposite thing because it want to detect those "failed" paths.
Note
My initial version of the algorithm stored the memoized results in a hash-map.
An std::vector is always faster at the cost of higher memory consumption, so I replaced it (see #define FAST).
I was surprised to see that the std::vector consumes actually 10% less memory while being 6 times faster.
Interactive test
You can submit your own input to my program and it will be instantly processed at my server:
This is equivalent toecho 25 | ./208
Output:
Note: the original problem's input 70 cannot be entered
because just copying results is a soft skill reserved for idiots.
(this interactive test is still under development, computations will be aborted after one second)
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
#include <iostream> #include <vector> #include <unordered_map> unsigned char numVisited[5] = { 0,0,0,0,0 }; unsigned char maxPerArc = 0; #define FAST #ifdef FAST const auto Unknown = 0xFFFFFFFFFFFFFFFFull; std::vector<unsigned long long> cache; #else std::unordered_map<unsigned int, unsigned long long> cache; #endif // count number of valid arcs
unsigned long long search(unsigned char arcsLeft = 70, unsigned char currentArc = 0) { // all arcs were used if (arcsLeft == 0) { // did not return to initial arc ? if (currentArc != 0) return 0; // expect that all arcs were visited equally often if (numVisited[0] != numVisited[1] || numVisited[2] != numVisited[3] || numVisited[0] != numVisited[2]) // no need to check visited[4] return 0; return 1; } // create a unique key const auto IdFactor = maxPerArc + 1; unsigned int id = currentArc; id *= IdFactor; id += numVisited[0]; id *= IdFactor; id += numVisited[1]; id *= IdFactor; id += numVisited[2]; id *= IdFactor; id += numVisited[3]; id *= IdFactor; id += numVisited[4]; // memoize #ifdef FAST if (cache.empty()) cache.resize(5 * IdFactor * IdFactor * IdFactor * IdFactor * IdFactor, Unknown); if (cache[id] != Unknown) return cache[id]; #else auto lookup = cache.find(id); if (lookup != cache.end()) return lookup->second; #endif unsigned long long result = 0; // turn left if possible auto turnLeft = (currentArc + 1) % 5; if (numVisited[turnLeft] < maxPerArc) { numVisited[turnLeft]++; result += search(arcsLeft - 1, turnLeft); numVisited[turnLeft]--; } // turn right if possible auto turnRight = (currentArc + 4) % 5; // -1 mod 5 => 5-1 mod 5 if (numVisited[turnRight] < maxPerArc) { numVisited[turnRight]++; result += search(arcsLeft - 1, turnRight); numVisited[turnRight]--; } // save result cache[id] = result; return result; } int main() { unsigned int numArcs = 70; std::cin >> numArcs; // let's go ! maxPerArc = numArcs / 5; std::cout << search(numArcs) << std::endl; return 0; }
This solution contains 12 empty lines, 10 comments and 10 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in 0.03 seconds on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
Peak memory usage was about 32 MByte.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
November 11, 2017 submitted solution
November 11, 2017 added comments
Difficulty
Project Euler ranks this problem at 70% (out of 100%).
Links
projecteuler.net/thread=208 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
Python github.com/nayuki/Project-Euler-solutions/blob/master/python/p208.py (written by Nayuki)
Python github.com/roosephu/project-euler/blob/master/208.py (written by Yuping Luo)
Python github.com/smacke/project-euler/blob/master/python/208.py (written by Stephen Macke)
C++ github.com/roosephu/project-euler/blob/master/208.cpp (written by Yuping Luo)
Java github.com/HaochenLiu/My-Project-Euler/blob/master/208.java (written by Haochen Liu)
Java github.com/nayuki/Project-Euler-solutions/blob/master/java/p208.java (written by Nayuki)
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 207 - Integer partition equations |

|
Circular Logic - problem 209 >> |