| << problem 407 - Idempotents |

|
Gnomon numbering - problem 412 >> |
Problem 411: Uphill paths
(see projecteuler.net/problem=411)
Let n be a positive integer. Suppose there are stations at the coordinates (x, y) = (2^i mod n, 3^i mod n) for 0 <= i <= 2n.
We will consider stations with the same coordinates as the same station.
We wish to form a path from (0, 0) to (n, n) such that the x and y coordinates never decrease.
Let S(n) be the maximum number of stations such a path can pass through.
For example, if n = 22, there are 11 distinct stations, and a valid path can pass through at most 5 stations.
Therefore, S(22) = 5. The case is illustrated below, with an example of an optimal path:
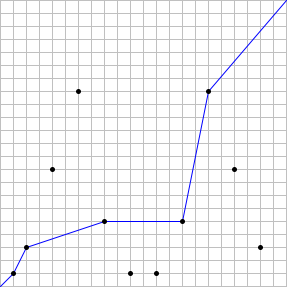
It can also be verified that S(123) = 14 and S(10000) = 48.
Find sum{S(k^5)} for 1 <= k <= 30.
Very inefficient solution
My code needs more than 60 seconds to find the correct result. (scroll down to the benchmark section)
Apparantly a much smarter algorithm exists - or my implementation is just inefficient.
My Algorithm
Generating the positions of all stations may look simple but there is a catch:
a large number of stations share the same position and thus all of them have to be treated as a single station.
STL's unique() function operates only on sorted data, therefore I need to call std::sort before it.
Actually I remove duplicates every now and then to keep memory consumption low.
When I looked at the number of stations before and after pruning duplicates I saw that these numbers stabilize after a while:
there are cycles which will generate the same stations over and over again.
My crude heuristic is to assume that if these numbers repeat then there is a cycle.
You can probably detect these cycles easier/earlier in a more mathematical way.
Then comes the fun part: finding the longest increasing subsequence (see en.wikipedia.org/wiki/Longest_increasing_subsequence)
The Wikipedia page has a nice description of an efficient O(n log n) algorithm (unlike the weird posting www.geeksforgeeks.org/longest-monotonically-increasing-subsequence-size-n-log-n/
and disturbingly ugly code at rosettacode.org/wiki/Longest_increasing_subsequence#C.2B.2B).
The core idea is simple:
- create an array
seqBackwhich will contain the last element (=back()of sequences) - those elements will be the smallest possible last elements among all sequences
- the first station is a sequence, too (with length = 1) and obviously the smallest possible so far, store it at
seqBack[0] - for each station: find the first station that is bigger ("northern")
- if there is no "bigger", then we just found a longer sequence, append it to
seqBack - replace the found station by the current station
- the number of elements in
seqBackis the longest subsequence
My first version of
getLIS() called std::lower_bound() because that's the default behavior of the algorithm.However, there may be multiple stations with different x- but identical y-component and therefore I had to change it to
std::upper_bound().
Note
My solution doesn't finish within one minute. OpenMP is enable if you uncomment #define PARALLEL.
Depending on your number of CPU cores, the solution is found in less than 60 seconds.
There are 19803868 unique stations for n = 29^5. I don't see how I can reduce the excessive memory consumption caused by that number.
Only be replacing std::vector by std::deque and a clever copying strategy I managed to get barely under 256 MByte.
And keep in mind that #define PARALLEL will further increase the memory usage.
Right now my solution to this problem is ranked number one in my list of most the "expensive" algorithms (see my performance ranking)
And finally I decided to create a template version of my function getLIS() in case I need it for other projects or problems.
Interactive test
You can submit your own input to my program and it will be instantly processed at my server:
This is equivalent toecho 10 | ./411
Output:
Note: the original problem's input 30 cannot be entered
because just copying results is a soft skill reserved for idiots.
(this interactive test is still under development, computations will be aborted after one second)
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
#include <iostream> #include <vector> #include <deque> #include <algorithm> // ---------- powmod from my toolbox ----------
// return (base^exponent) % modulo for 32-bit values, no need for mulmod
unsigned int powmod(unsigned int base, unsigned int exponent, unsigned int modulo) { unsigned int result = 1; while (exponent > 0) { // fast exponentation: // odd exponent ? a^b = a*a^(b-1) if (exponent & 1) result = (result * (unsigned long long)base) % modulo; // even exponent ? a^b = (a*a)^(b/2) base = (base * (unsigned long long)base) % modulo; exponent >>= 1; } return result; } // ---------- problem-specific code ----------
// a 2D point
struct Location { // coordinates unsigned int x; unsigned int y; // create new point Location(unsigned int x_ = 0, unsigned y_ = 0) : x(x_), y(y_) {} // return point at (2^index % modulo, 3^index % modulo) static Location generate(unsigned int index, unsigned int modulo) { auto x = powmod(2, index, modulo); auto y = powmod(3, index, modulo); return Location(x, y); } // for sorting bool operator<(const Location& other) const { if (x != other.x) return x < other.x; else return y < other.y; } // for sorting bool operator==(const Location& other) const { return x == other.x && y == other.y; } }; // return length of longest increasing subsequence
template <typename T> unsigned int getLIS(T first, T last) // begin/end of a container { // no data ? if (first == last) return 0; // seqBack[i] contains the smallest last element of a subsequence with length i + 1 (plus one because buffer is zero-indexed) std::vector<typename T::value_type> seqBack; seqBack.reserve(1 << 16); // initialize subsequence with length = 1 with the first element seqBack.push_back(*first++); while (first != last) { // locate shortest sequence where the last element >= current element auto current = *first++; auto pos = std::upper_bound(seqBack.begin(), seqBack.end(), current); // current element is the largest element observed so far ? => it extends the longest sequence if (pos == seqBack.end()) seqBack.push_back(current); else // current element is smaller for that sequence length => "optimize" *pos = current; // could skip this step if *pos == current } return seqBack.size(); } // compute S(n)
unsigned int minPathLength(unsigned int n) { // generate all stations std::deque<Location> stations; //if (n > 10000000) //stations.reserve(n * 1.05); size_t lastUnsortedSize = 0; size_t lastSortedSize = 0; for (unsigned int i = 0; i <= 2 * n; i++) { auto current = Location::generate(i, n); // the route always starts at (0,0) so discard any stations placed there if (current.x == 0 && current.y == 0) continue; stations.push_back(current); // 0x100000 is the sweet spot: // - if I remove duplicates more often, then I spent too much time sorting // - if I remove duplicates less often, then memory consumption grows (and sort/unique slow down as well) if (i % 0x100000 == 0 && i > 0) { // prune duplicates std::sort(stations.begin(), stations.end()); auto garbage = std::unique(stations.begin(), stations.end()); size_t unsortedSize = stations.size(); size_t sortedSize = std::distance(stations.begin(), garbage); stations.erase(garbage, stations.end()); // same sizes as in last pass ? => assume that we entered a cycle/loop if (unsortedSize == lastUnsortedSize && sortedSize == lastSortedSize) break; lastUnsortedSize = unsortedSize; lastSortedSize = sortedSize; } } // prune duplicates std::sort(stations.begin(), stations.end()); auto garbage = std::unique(stations.begin(), stations.end()); stations.erase(garbage, stations.end()); // reduce locations to their y-components std::vector<unsigned int> onlyY; // simple but memory consuming //for (auto station : stations) // onlyY.push_back(station.y); // a bit slower but keeps me below 256 MByte while (!stations.empty()) { onlyY.push_back(stations.begin()->y); stations.erase(stations.begin()); } // find shortest route return getLIS(onlyY.begin(), onlyY.end()); } int main() { unsigned int limit = 30; std::cin >> limit; unsigned int sum = 0; //#define PARALLEL
#ifdef PARALLEL #pragma omp parallel for reduction(+:sum) schedule(dynamic) #endif for (int k = limit; k >= 1; k--) // run loop in reverse to optimize load for OpenMP // evaluate k^5 sum += minPathLength(k*k*k*k*k); std::cout << sum << std::endl; return 0; }
This solution contains 25 empty lines, 37 comments and 7 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in 92 seconds (exceeding the limit of 60 seconds).
The code can be accelerated with OpenMP but the timings refer to the single-threaded version on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
Peak memory usage was about 235 MByte.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
October 5, 2017 submitted solution
October 5, 2017 added comments
Difficulty
Project Euler ranks this problem at 45% (out of 100%).
Links
projecteuler.net/thread=411 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
Python github.com/Meng-Gen/ProjectEuler/blob/master/411.py (written by Meng-Gen Tsai)
C++ github.com/smacke/project-euler/blob/master/cpp/411.cpp (written by Stephen Macke)
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 407 - Idempotents |

|
Gnomon numbering - problem 412 >> |