| << problem 411 - Uphill paths |

|
Factorisation triples - problem 418 >> |
Problem 412: Gnomon numbering
(see projecteuler.net/problem=412)
For integers m, n (0 <= n < m), let L(m, n) be an m * m grid with the top-right n * n grid removed.
For example, L(5, 3) looks like this:
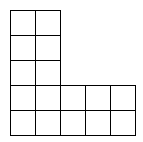
We want to number each cell of L(m, n) with consecutive integers 1, 2, 3, ... such that the number in every cell is smaller than the number below it and to the left of it.
For example, here are two valid numberings of L(5, 3):

Let LC(m, n) be the number of valid numberings of L(m, n).
It can be verified that LC(3, 0) = 42, LC(5, 3) = 250250, LC(6, 3) = 406029023400 and LC(10, 5) mod 76543217 = 61251715.
Find LC(10000, 5000) mod 76543217.
Not solved yet
My code works for the "small" example but can't find the solution to the "big" problem.
What I've Done So Far
Okay, at the moment I have no idea how to solve that problem.
But it was fun spending a few minutes on writing a brute-force solution for grids no larger than 6x6.
By the way: bruteForce(6,3) finished after about 7.5 hours ...
The next morning I wrote slow which is based on the following observation:
- when filling the grid "in reverse order" (that means from 16 to 1), then smaller numbers are automatically stacked on larger numbers
- each column of the grid can be seen as a "skyscraper"
- there are no gaps in a skyscraper
- each skyscraper is at most as high as its left neighbor
Instead I just need to track the height of each skyscraper (a 1D data structure).
These heights are identical for many different number distributions so that I can accelerate the search by aggressive memoization.
slow(6,3) finds the correct result in less than 0.01 seconds (vs. 7.5 hours !).Note: all results are displayed mod 76543217.
However, this improved algorithm can't solve LC(10000, 5000) in a reasonable timeframe.
Interactive test
You can submit your own input to my program and it will be instantly processed at my server:
This is equivalent toecho "10 5" | ./412
Output:
(this interactive test is still under development, computations will be aborted after one second)
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
#include <iostream> #include <vector> #include <map> const auto MaxSize = 10; // no grids larger than 10x10 (6x6 is already super-slow in brute-force mode) auto size = 5; // that's m from the problem statement auto cutout = 3; // that's n from the problem statement const auto Modulo = 76543217; // indicates a cell that hasn't be filled yet
const unsigned int Unknown = 0; unsigned int cells[MaxSize][MaxSize] = { Unknown }; // add "number" and all smaller numbers to "cells", return how many combinations where found
unsigned long long bruteForce(unsigned int number) { // successfully filled all cells ? if (number == 0) { static unsigned long long progress = 0; if (++progress % (1 << 24) == 0) std::cout << (progress * 100.0 / 406029023400) << "%" << std::endl; return 1; } unsigned long long result = 0; // iterate over all free spots where the left and lower neighbor are bigger (or there is no neighbor => border) for (auto y = 0; y < size; y++) { // avoid the cut-out area auto maxX = size; if (y < cutout) maxX = size - cutout; for (auto x = 0; x < maxX; x++) { // cell previously filled ? if (cells[x][y] != Unknown) continue; // all bigger numbers were already processed, so there's no gap allowed on the left or bottom // left neighbor must exist, or there's the grid's border if (x > 0 && cells[x-1][y] == Unknown) continue; // bottom neighbor must exist, or there's the grid's border if (y < size - 1 && cells[x][y+1] == Unknown) continue; // okay, found an empty cell ! cells[x][y] = number; // go deeper result += bruteForce(number - 1); // undo current step and keep looking for other configurations cells[x][y] = Unknown; } } return result % Modulo; } // my "skyscraper" algorithm
typedef std::vector<unsigned short> HeightMap; unsigned long long slow(unsigned int number, HeightMap& height) { // successfully filled all cells ? if (number == 1) return 1; // memoize static std::map<HeightMap, unsigned long long> cache; auto lookup = cache.find(height); if (lookup != cache.end()) return lookup->second; // find a column that isn't full and is lower than its left neighbor unsigned long long result = 0; for (auto i = 0; i < size; i++) { // maximum height auto maxHeight = size; if (i >= size - cutout) maxHeight -= cutout; if (height[i] < maxHeight) // lower than its left neighbor ? if (i == 0 || height[i] < height[i - 1]) { height[i]++; result += slow(number - 1, height); height[i]--; } } result %= Modulo; cache[height] = result; return result; } int main() { std::cin >> size >> cutout; // for live tests only if (size > MaxSize || size < cutout) return 1; // the highest number is always located in the lower-right corner auto highestNumber = size * size - cutout * cutout; // brute force //std::cout << bruteForce(highestNumber) << std::endl; // significantly faster, but still too slow to solve the problem (it easily solves all examples) HeightMap height(size, 0); std::cout << slow(highestNumber, height) << std::endl; return 0; }
This solution contains 22 empty lines, 23 comments and 3 preprocessor commands.
Changelog
December 22, 2017 solve grids up to 6x6
Difficulty
Project Euler ranks this problem at 50% (out of 100%).
Links
projecteuler.net/thread=412 - the best forum on the subject (note: you have to submit the correct solution first)
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 411 - Uphill paths |

|
Factorisation triples - problem 418 >> |