| << problem 67 - Maximum path sum II |

|
Totient maximum - problem 69 >> |
Problem 68: Magic 5-gon ring
(see projecteuler.net/problem=68)
Consider the following "magic" 3-gon ring, filled with the numbers 1 to 6, and each line adding to nine.
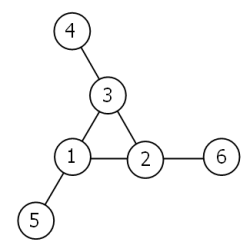
Working clockwise, and starting from the group of three with the numerically lowest external node (4,3,2 in this example),
each solution can be described uniquely. For example, the above solution can be described by the set: 4,3,2; 6,2,1; 5,1,3.
It is possible to complete the ring with four different totals: 9, 10, 11, and 12. There are eight solutions in total.
TotalSolution Set
94,2,3; 5,3,1; 6,1,2
94,3,2; 6,2,1; 5,1,3
102,3,5; 4,5,1; 6,1,3
102,5,3; 6,3,1; 4,1,5
111,4,6; 3,6,2; 5,2,4
111,6,4; 5,4,2; 3,2,6
121,5,6; 2,6,4; 3,4,5
121,6,5; 3,5,4; 2,4,6
By concatenating each group it is possible to form 9-digit strings; the maximum string for a 3-gon ring is 432621513.
Using the numbers 1 to 10, and depending on arrangements, it is possible to form 16- and 17-digit strings. What is the maximum 16-digit string for a "magic" 5-gon ring?
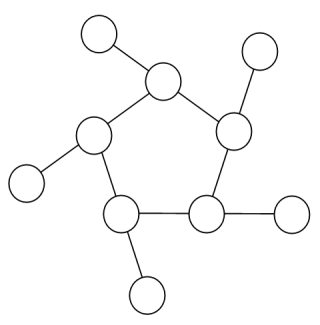
My Algorithm
I split the graph into two parts:
- an "inner ring"
- and an "outer ring"
Each cell of the inner ring is part of two lines. It is indexed from
0 to size - 1 (size is 3 for a 3-gon, 5 for a 5-gon, etc.).Each cell of the outer ring is part of only one line. It is indexed from
size to 2*size - 1.The idea is to fill the inner ring using backtracking.
Whenever two out of three cells of a line are known, the third can be directly computed.
If that third number is already used, then we have to backtrack.
My function
fillLine fills the inner ring: it tries all combination of available numbers for the cell at index pos.Whenever it succeeds, it calls itself (recursion) to fill
pos + 1.All available numbers are stored in a bitmask called
used. Number x is available if (used & (1 << x)) == 0.At the end,
result contains all valid n-gons.Project Euler asks for the maximum string while Hackerrank asks for all strings in ascending order.
My solution prints the Hackerrank result and I manually have to choose the larger one (there are just two solutions).
The correct result will be printed when
size = 5 and tripletSum = 14, that means the program input is "5 14".There are solutions for
"5 16", "5 17" and "5 19" but they are either lexicographically smaller or have 17 instead of 16 digits.
Interactive test
You can submit your own input to my program and it will be instantly processed at my server:
This live test is based on the Hackerrank problem.
This is equivalent toecho "3 9" | ./68
Output:
Note: the original problem's input 5 14 cannot be entered
because just copying results is a soft skill reserved for idiots.
(this interactive test is still under development, computations will be aborted after one second)
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
The code contains #ifdefs to switch between the original problem and the Hackerrank version.
Enable #ifdef ORIGINAL to produce the result for the original problem (default setting for most problems).
#include <iostream> #include <vector> #include <string> #include <set> // sorted container of valid n-gon strings
std::set<std::string> result; // size of the n-gon (3,4,5)
unsigned int size; // sum of all three cells alongs a diagonal/edge
unsigned int tripletSum; void fillLine(unsigned int pos, std::vector<unsigned int> inner, std::vector<unsigned int> outer, unsigned int used) { // inner ring completely filled, just one cell of the outer ring left if (pos == size - 1) { // check last line outer[size - 1] = tripletSum - (inner[0] + inner[size - 1]); unsigned int mask = 1 << outer[size - 1]; if ((used & mask) != 0) return; // first element of outer ring must be the smallest for (auto x : outer) if (x < outer[0]) return; // build string std::string id; for (unsigned int i = 0; i < size; i++) id += std::to_string(outer[i]) + std::to_string(inner[i]) + std::to_string(inner[(i + 1) % size]); // will be alphabetically ordered result.insert(id); return; } // move a number between 1 and 2*size into one of the inner cells of the n-gon for (unsigned int i = 1; i <= 2*size; i++) { // fill a cell of the inner ring unsigned int innerMask = 1 << i; // is that number still available ? if ((innerMask & used) != 0) continue; // occupy cell inner[pos + 1] = i; unsigned int nextUsed = used | innerMask; // compute the according cell in the outer ring outer[pos] = tripletSum - (inner[pos] + i); unsigned int outerMask = 1 << outer[pos]; // is that number still available ? if ((nextUsed & outerMask) != 0) continue; nextUsed |= outerMask; // next line fillLine(pos + 1, inner, outer, nextUsed); } } int main() { std::cin >> size >> tripletSum; // generate the inner and outer ring std::vector<unsigned int> inner(size); std::vector<unsigned int> outer(size); // a triplet consists of inner[a], inner[(a+1) % (2*a)], outer[a] // generate a bitmask of allowed numbers (0 = still available, 1 = already used / disallowed) unsigned int allowed = 0; for (unsigned int i = 1; i <= 2 * size; i++) allowed |= 1 << i; allowed = ~allowed; // fill first cell of inner ring for (unsigned int i = 1; i <= 2*size; i++) { inner[0] = i; // fill remaining cells fillLine(0, inner, outer, allowed | (1 << i)); } //#define ORIGINAL
#ifdef ORIGINAL std::cout << *result.rbegin() << std::endl; #else for (auto r : result) std::cout << r << std::endl; #endif }
This solution contains 14 empty lines, 21 comments and 7 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in less than 0.01 seconds on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
March 13, 2017 submitted solution
May 2, 2017 added comments
Hackerrank
see https://www.hackerrank.com/contests/projecteuler/challenges/euler068
My code solves 22 out of 22 test cases (score: 100%)
Difficulty
Project Euler ranks this problem at 25% (out of 100%).
Hackerrank describes this problem as hard.
Note:
Hackerrank has strict execution time limits (typically 2 seconds for C++ code) and often a much wider input range than the original problem.
In my opinion, Hackerrank's modified problems are usually a lot harder to solve. As a rule thumb: brute-force is rarely an option.
Links
projecteuler.net/thread=68 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
C# www.mathblog.dk/project-euler-68-what-is-the-maximum-16-digit-string-for-a-magic-5-gon-ring/ (written by Kristian Edlund)
Python github.com/hughdbrown/Project-Euler/blob/master/euler-068.py (written by Hugh Brown)
Python github.com/nayuki/Project-Euler-solutions/blob/master/python/p068.py (written by Nayuki)
Python github.com/smacke/project-euler/blob/master/python/68.py (written by Stephen Macke)
C++ github.com/HaochenLiu/My-Project-Euler/blob/master/068.cpp (written by Haochen Liu)
C++ github.com/Meng-Gen/ProjectEuler/blob/master/68.cc (written by Meng-Gen Tsai)
C++ github.com/roosephu/project-euler/blob/master/68.cpp (written by Yuping Luo)
Java github.com/dcrousso/ProjectEuler/blob/master/PE068.java (written by Devin Rousso)
Java github.com/nayuki/Project-Euler-solutions/blob/master/java/p068.java (written by Nayuki)
Go github.com/frrad/project-euler/blob/master/golang/Problem068.go (written by Frederick Robinson)
Mathematica github.com/steve98654/ProjectEuler/blob/master/068.nb
Clojure github.com/rm-hull/project-euler/blob/master/src/euler068.clj (written by Richard Hull)
Scala github.com/samskivert/euler-scala/blob/master/Euler068.scala (written by Michael Bayne)
Perl github.com/gustafe/projecteuler/blob/master/068-Magic-5-gon-ring.pl (written by Gustaf Erikson)
Rust github.com/gifnksm/ProjectEulerRust/blob/master/src/bin/p068.rs
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 67 - Maximum path sum II |

|
Totient maximum - problem 69 >> |