| << problem 137 - Fibonacci golden nuggets |

|
Pythagorean tiles - problem 139 >> |
Problem 138: Special isosceles triangles
(see projecteuler.net/problem=138)
Consider the isosceles triangle with base length, b = 16, and legs, L = 17.
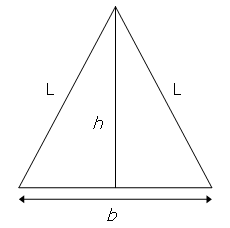
By using the Pythagorean theorem it can be seen that the height of the triangle, h = sqrt{172 - 82} = 15, which is one less than the base length.
With b = 272 and L = 305, we get h = 273, which is one more than the base length, and this is the second smallest isosceles triangle with the property that h = b \pm 1.
Find sum{L} for the twelve smallest isosceles triangles for which h = b \pm 1 and b, L are positive integers.
My Algorithm
Even though I felt right from the start that brute force can solve this problem, I tried it anyways.
And within a few seconds the function bruteForce displayed these 7 solutions:
17, 305, 5473, 98209, 1762289, 31622993, 567451585
I wasn't willing to dig deep into mathematical territory and decided to look hard at those numbers ...
and yes, a pattern revealed:
17
305 = 17*18 - 1
5473 = 305*18 - 17
98209 = 5473*18 - 305
1762289 = 98209*18 - 5473
31622993 = 1762289*18 - 98209
567451585 = 31622993*18 - 1762289
That's a surprisingly simple series:
x_0 = 1
x_1 = 17
x_n = x_{n-1} * 18 - x_{n-2}
My code looks a bit messy because of the Hackerrank modifications.
Alternative Approaches
You can apply Pell's equation to discover this sequence without "taking a hard look".
And many Fibonacci numbers pop up along the way ...
Modifications by HackerRank
Not only 12 but up to 10^18 triangles have to be found.
My code precomputes the first 100000 triangles (enough to pass 3 out of 4 test cases) and then
performs a simple lookup.
All numbers have to be modulo 10^9+7.
Interactive test
You can submit your own input to my program and it will be instantly processed at my server:
This is equivalent toecho "1 2" | ./138
Output:
Note: the original problem's input 12 cannot be entered
because just copying results is a soft skill reserved for idiots.
(this interactive test is still under development, computations will be aborted after one second)
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
The code contains #ifdefs to switch between the original problem and the Hackerrank version.
Enable #ifdef ORIGINAL to produce the result for the original problem (default setting for most problems).
#include <iostream> #include <vector> #include <cmath> #define ORIGINAL // find the first sevens solutions in a few seconds
void bruteForce(long long limit) { for (long long base = 2; base < limit; base += 2) { // both right-angled triangles with side lengths L, h, half auto half = base / 2; // two potential solutions auto height1 = base - 1; auto height2 = base + 1; // compute L1 and L2 auto triangle1 = half * half + height1 * height1; long long hypo1 = sqrt(triangle1); if (hypo1 * hypo1 == triangle1) std::cout << hypo1 << " => b=" << base << " h=" << height1 << " diff=" << (base - height1) << std::endl; auto triangle2 = half * half + height2 * height2; long long hypo2 = sqrt(triangle2); if (hypo2 * hypo2 == triangle2) std::cout << hypo2 << " => b=" << base << " h=" << height2 << " diff=" << (base - height2) << std::endl; } } int main() { // precompute the first 10^6 solutions std::vector<unsigned long long> solutions; // the first seven solutions reveal a pattern ... // 17 // 305 = 17*18 - 1 // 5473 = 305*18 - 17 // 98209 = 5473*18 - 305 // 1762289 = 98209*18 - 5473 // 31622993 = 1762289*18 - 98209 // 567451585 = 31622993*18 - 1762289 #ifdef ORIGINAL const unsigned int MaxPrecompute = 12; #else const unsigned int MaxPrecompute = 1000000; #endif // first solution is 17 long long current = 17; solutions.push_back(current); // add it to the total long long sum = current; // previous solution ("zero-th" solution is 1 long long previous = 1; for (unsigned int i = 2; i <= MaxPrecompute; i++) { // one more step ... auto next = current * 18 - previous; #ifndef ORIGINAL // prevent negative numbers const long long Modulo = 1000000007; if (next < 0) next += Modulo; #endif // next => current => previous previous = current; current = next; // add solution sum += current; #ifndef ORIGINAL // keep only residue sum %= Modulo; current %= Modulo; #endif // store solution solutions.push_back(sum); } unsigned int tests = 1; std::cin >> tests; while (tests--) { unsigned long long smallest = 12; std::cin >> smallest; auto index = smallest - 1; // not pre-computed ? => abort if (index >= solutions.size()) return 0; // look up result std::cout << solutions[index] << std::endl; } return 0; }
This solution contains 19 empty lines, 24 comments and 11 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in less than 0.01 seconds on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
July 10, 2017 submitted solution
July 10, 2017 added comments
Hackerrank
see https://www.hackerrank.com/contests/projecteuler/challenges/euler138
My code solves 4 out of 5 test cases (score: 66.67%)
I failed 0 test cases due to wrong answers and 1 because of timeouts
Difficulty
Project Euler ranks this problem at 45% (out of 100%).
Hackerrank describes this problem as easy.
Note:
Hackerrank has strict execution time limits (typically 2 seconds for C++ code) and often a much wider input range than the original problem.
In my opinion, Hackerrank's modified problems are usually a lot harder to solve. As a rule thumb: brute-force is rarely an option.
Links
projecteuler.net/thread=138 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
C# www.mathblog.dk/project-euler-138-special-isosceles-triangles/ (written by Kristian Edlund)
C# github.com/HaochenLiu/My-Project-Euler/blob/master/138.cs (written by Haochen Liu)
Python github.com/hughdbrown/Project-Euler/blob/master/euler-138.py (written by Hugh Brown)
Python github.com/smacke/project-euler/blob/master/python/138.py (written by Stephen Macke)
C++ github.com/Meng-Gen/ProjectEuler/blob/master/138.cc (written by Meng-Gen Tsai)
C++ github.com/roosephu/project-euler/blob/master/138.cpp (written by Yuping Luo)
Java github.com/dcrousso/ProjectEuler/blob/master/PE138.java (written by Devin Rousso)
Java github.com/thrap/project-euler/blob/master/src/Java/Problem138.java (written by Magnus Solheim Thrap)
Go github.com/frrad/project-euler/blob/master/golang/Problem138.go (written by Frederick Robinson)
Mathematica github.com/steve98654/ProjectEuler/blob/master/138.nb
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 137 - Fibonacci golden nuggets |

|
Pythagorean tiles - problem 139 >> |