| << problem 286 - Scoring probabilities |

|
An enormous factorial - problem 288 >> |
Problem 287: Quadtree encoding (a simple compression algorithm)
(see projecteuler.net/problem=287)
The quadtree encoding allows us to describe a 2^N * 2^N black and white image as a sequence of bits (0 and 1).
Those sequences are to be read from left to right like this:
- the first bit deals with the complete 2^N * 2^N region;
- "0" denotes a split: the current 2^n * 2^n region is divided into 4 sub-regions of dimension 2^{n-1} * 2^{n-1},
- "10" indicates that the current region contains only black pixels;
- "11" indicates that the current region contains only white pixels.
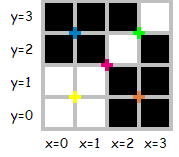
This image can be described by several sequences, for example : "001010101001011111011010101010", of length 30, or
"0100101111101110", of length 16, which is the minimal sequence for this image.
For a positive integer N, define D_N as the 2^N * 2^N image with the following coloring scheme:
the pixel with coordinates x = 0, y = 0 corresponds to the bottom left pixel,
if (x - 2^{N-1})^2 + (y - 2^{N-1})^2 <= 2^{2N-2} then the pixel is black,
otherwise the pixel is white.
What is the length of the minimal sequence describing D_24 ?
My Algorithm
The given formula can be easily translated to a function isBlack(x,y) that returns true if the pixel at (x,y) is black.
It looks like the equation of a circle - and when printing D_4 on screen I get (see #ifdef DRAW_IMAGE):
.....BBBBBBB....
...BBBBBBBBBBB..
..BBBBBBBBBBBBB.
..BBBBBBBBBBBBB.
.BBBBBBBBBBBBBBB
.BBBBBBBBBBBBBBB
.BBBBBBBBBBBBBBB
BBBBBBBBBBBBBBBB
.BBBBBBBBBBBBBBB
.BBBBBBBBBBBBBBB
.BBBBBBBBBBBBBBB
..BBBBBBBBBBBBB.
..BBBBBBBBBBBBB.
...BBBBBBBBBBB..
.....BBBBBBB....
........B.......
The combination of a circle and rectangles has some nice properties:
- if all four corners of the rectangle are inside the circle (= black) then the whole rectangle is black
- if the rectangle is much smaller than the circle and all fours corners of the rectangle are outside the circle then the whole rectangle is outside the circle
encode returns the size of an optimal encoding and performs the following tasks in a recursive manner:- if the current square covers only 1 pixel then it needs 2 bits
- check all four corners of the current square, if they are all inside or outside then its encoding requires 2 bits
- subdivide the current square into 4 equally-sized squares and determine their encoding size plus 1 bit for the split
Note
When the current square is 2x2 and some of its corner are black and some are white then I know that these four pixels need 1 + 2+2+2+2 bits, saving one recursion step (about 10% faster).
The encoded image has a compression ratio of about 900000 to 1. That's excellent - photos usually compress to about 10:1.
Interactive test
You can submit your own input to my program and it will be instantly processed at my server:
This is equivalent toecho 4 | ./287
Output:
Note: the original problem's input 24 cannot be entered
because just copying results is a soft skill reserved for idiots.
(this interactive test is still under development, computations will be aborted after one second)
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
#include <iostream> // D24 => 2^24
unsigned int size = 1 << 24; // return true if pixel at (x,y) is black
bool isBlack(unsigned int x, unsigned int y) { // 2^(N-1) long long middle = size >> 1; // right side of the equation: 2^(2N - 2) = 2^(N-1) * 2^(N-1) = middle * middle auto threshold = middle * middle; // be a bit careful with negative differences auto dx = (long long)x - middle; auto dy = (long long)y - middle; return dx*dx + dy*dy <= threshold; } // return size of optimal encoding // note: I expect only valid input, such that (toX - fromX) = (toY - fromY) = a power of two
unsigned int encode(unsigned int fromX, unsigned int fromY, unsigned int toX, unsigned int toY, bool isFirst = true) { // a single pixel ? if (fromX == toX) // implies fromY == toY return 2; // doesn't matter whether black or white, both encodings need two bits // isBlack() will produce a black circle // checking all four corners is sufficient to know when to split bool a = isBlack(fromX, fromY); bool b = isBlack(toX, fromY); bool c = isBlack(toX, toY); bool d = isBlack(fromX, toY); // same color on all four corner => the whole area is covered by the same color // however, this assumption doesn't hold on the first level if (a == b && b == c && c == d && !isFirst) return 2; // again: the color doesn't matter, both need two bits to fill the entire area // speed optimization: if a 2x2 area needs to be split, then it always requires 9 bits if (fromX + 1 == toX) return 1 + 4*2; // a split marker and four single pixels (2 bits each) // split evenly auto half = (toX - fromX + 1) / 2; return encode(fromX, fromY + half, toX - half, toY, false) + // upper-left encode(fromX + half, fromY + half, toX, toY, false) + // upper-right encode(fromX, fromY, toX - half, toY - half, false) + // lower-left encode(fromX + half, fromY, toX, toY - half, false) + // lower-right 1; // don't forget: there's one bit for the split marker } int main() { // D24 => 24 unsigned int shift = 4; std::cin >> shift; // length of an edge of the image in pixels size = 1 << shift; // draw on screen (only useful for very small values of "shift" 1 ... 5) #define DRAW_IMAGE #ifdef DRAW_IMAGE if (size <= 5) { for (unsigned int y = 0; y < size; y++) { auto flipY = (size - 1) - y; // problem states that lower-left corner is (0,0), must flip image upside-down for (unsigned int x = 0; x < size; x++) std::cout << (isBlack(x, flipY) ? "B" : "."); std::cout << std::endl; } } #endif // let's compress to infinity and beyond ! std::cout << encode(0, 0, size - 1, size - 1) << std::endl; return 0; }
This solution contains 12 empty lines, 18 comments and 4 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in 0.8 seconds on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
August 29, 2017 submitted solution
August 29, 2017 added comments
Difficulty
Project Euler ranks this problem at 40% (out of 100%).
Links
projecteuler.net/thread=287 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
C++ github.com/smacke/project-euler/blob/master/cpp/287.cpp (written by Stephen Macke)
C github.com/LaurentMazare/ProjectEuler/blob/master/e287.c (written by Laurent Mazare)
Java github.com/thrap/project-euler/blob/master/src/Java/Problem287.java (written by Magnus Solheim Thrap)
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 286 - Scoring probabilities |

|
An enormous factorial - problem 288 >> |