| << problem 601 - Divisibility streaks |

|
Roman Numerals II - problem 610 >> |
Problem 607: Marsh Crossing
(see projecteuler.net/problem=607)
Frodo and Sam need to travel 100 leagues due East from point A to point B. On normal terrain, they can cover 10 leagues per day, and so the journey would take 10 days.
However, their path is crossed by a long marsh which runs exactly South-West to North-East, and walking through the marsh will slow them down.
The marsh is 50 leagues wide at all points, and the mid-point of AB is located in the middle of the marsh.
A map of the region is shown in the diagram below:
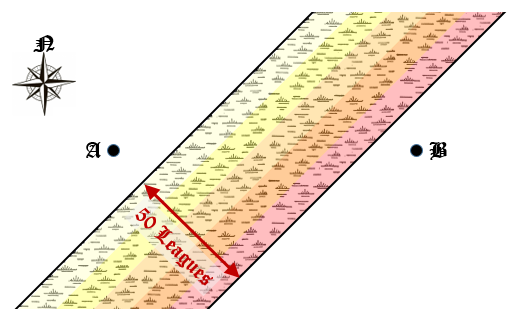
The marsh consists of 5 distinct regions, each 10 leagues across, as shown by the shading in the map.
The strip closest to point A is relatively light marsh, and can be crossed at a speed of 9 leagues per day.
However, each strip becomes progressively harder to navigate, the speeds going down to 8, 7, 6 and finally 5 leagues per day for the final region of marsh,
before it ends and the terrain becomes easier again, with the speed going back to 10 leagues per day.
If Frodo and Sam were to head directly East for point B, they would travel exactly 100 leagues, and the journey would take approximately 13.4738 days.
However, this time can be shortened if they deviate from the direct path.
Find the shortest possible time required to travel from point A to B, and give your answer in days, rounded to 10 decimal places.
My Algorithm
Each section of the marsh is leagues wide. However, walking the direct route means they walk sqrt{2} * 10 approx 14.1421 leagues in each section.
In order to be faster they should walk less than 14.1421 leagues in each slow section and walk a longer distance on the normal terrain.
The whole map is a two-dimensional coordinate system. Initially I tried to have city A at (0,0) and B at (100,0) but things got messy.
Then I decided to rotate the whole map by 45 degrees such that the marsh is parallel to the y-axis.
City A still remains at (0,0) while B is located at (dfrac{100}{sqrt{2}}, dfrac{100}{sqrt{2}}).
The distance between both cities is still 100 leagues.
Knowing that the marsh is exactly 50 leagues wide, the marsh' smallest x and largest x are 50 units apart.
Since x_B - x_A = dfrac{100}{sqrt{2}} - 0 approx 70.7107 the marsh starts at x_1 approx (70.7107 - 50) / 2 approx 10.3553.
The next crossing will be at x_2 = x_1 + 10, then x_3 = x_2 + 10, ..., x_6 = x_5 + 10 = x_1 + 50.
The direct route is x = y and will be stored in my container named points.
The function duration() determines the distance between consecutive points and divide them by the speed of Frodo and Sam (see speed).
It returns 13.4738023615 for the direct route.
I like Monte-Carlo simulations because even though they seem to be unpredictable they produce a predictable result after some time.
This problem can be solved by randomizing the y-components of the marsh:
mutatepicks a random point out ofpoints, except for the first and last (A and B)- it randomly adds or subtracts a given
delta - if
duration()returns a shorter time than before then keep this mutation, else undo it
delta and successively reduces it.The way I reduce
delta and how often I call mutate() is not scientific at all:I started with many more iterations and a slower decrease but saw that the coarser values still produce the correct result.
Alternative Approaches
The Gradient Descent method is a more straightforward optimization method (see en.wikipedia.org/wiki/Gradient_descent).
The problem can be solved with Snell's law, too (see en.wikipedia.org/wiki/Snell's_law).
Interactive test
This feature is not available for the current problem.
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
#include <iostream> #include <iomanip> #include <vector> #include <cmath> // crossing between two marches
struct Point { double x; double y; // create a new 2D point Point(double x_, double y_) : x(x_), y(y_) {} // distance between two points double distance(const Point& other) const { auto diffX = x - other.x; auto diffY = y - other.y; return sqrt(diffX * diffX + diffY * diffY); } }; // how many days does it take to walk from the first to the last point, considering "speed" of the surfaces
double duration(const std::vector<Point>& points) { // leagues travelled per day between point[i] and point[i+1] static const std::vector<double> speed = { 10, 9, 8, 7, 6, 5, 10 }; double result = 0; // for each surface: determine length and divide by speed for (size_t i = 0; i < speed.size(); i++) { auto way = points[i].distance(points[i+1]); result += way / speed[i]; } return result; } // a simple pseudo-random number generator // (produces the same result no matter what compiler you have - unlike rand() from math.h)
unsigned int myrand() { static unsigned long long seed = 0; seed = 6364136223846793005ULL * seed + 1; return (unsigned int)(seed >> 30); } // try to move a single point's y-value by delta // if the mutation is better, then keep the result // if the mutation is worse, then undo the change
void mutate(std::vector<Point>& points, double delta) { auto oldDuration = duration(points); // decide at random whether to add or subtract if (myrand() & 1) delta = -delta; // change one random y-coordinate (must not be the first or last) auto id = myrand() % 6 + 1; points[id].y += delta; // not faster ? => undo change if (duration(points) >= oldDuration) points[id].y -= delta; } int main() { // A std::vector<Point> points; points.push_back({ 0, 0 }); // rotate the coordinate system by 45 degrees, // so that travelling one league is equivalent to moving 1/scaling units along x-axis and 1/scaling units along y-axis double scaling = sqrt(2); // when travelling the shortest distance between A and B, how wide is the marsh ? auto direct = 50 * scaling; // c^2 = a^2 + b^2 where a=b=50 // entering the marsh auto current = ((100 - direct) / 2) / scaling; // same as 25*(sqrt(2)-1) points.push_back({ current, current }); // all 5 zones of the marsh for (auto i = 1; i <= 5; i++) points.push_back({ current + i * 10, current + i * 10 }); // B points.push_back({ 100 / scaling, 100 / scaling }); // randomly mutate the crossing const auto NumIterations = 10000; for (auto delta = 0.01; delta >= 0.00001; delta /= 10) for (auto i = 0; i < NumIterations; i++) mutate(points, delta); // display result with 10 digits after the decimal point std::cout << std::fixed << std::setprecision(10) << duration(points) << std::endl; return 0; }
This solution contains 18 empty lines, 23 comments and 4 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in less than 0.01 seconds on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
October 18, 2017 submitted solution
October 18, 2017 added comments
Links
projecteuler.net/thread=607 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
Python github.com/Meng-Gen/ProjectEuler/blob/master/607.py (written by Meng-Gen Tsai)
Python github.com/smacke/project-euler/blob/master/python/607.py (written by Stephen Macke)
Sage github.com/roosephu/project-euler/blob/master/607.sage (written by Yuping Luo)
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 601 - Divisibility streaks |

|
Roman Numerals II - problem 610 >> |