| << problem 304 - Primonacci |

|
Chip Defects - problem 307 >> |
Problem 306: Paper-strip Game
(see projecteuler.net/problem=306)
The following game is a classic example of Combinatorial Game Theory:
Two players start with a strip of n white squares and they take alternate turns.
On each turn, a player picks two contiguous white squares and paints them black.
The first player who cannot make a move loses.
- If n = 1, there are no valid moves, so the first player loses automatically.
- If n = 2, there is only one valid move, after which the second player loses.
- If n = 3, there are two valid moves, but both leave a situation where the second player loses.
- If n = 4, there are three valid moves for the first player; she can win the game by painting the two middle squares.
- If n = 5, there are four valid moves for the first player (shown below in red); but no matter what she does, the second player (blue) wins.
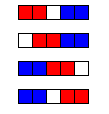
So, for 1 <= n <= 5, there are 3 values of n for which the first player can force a win.
Similarly, for 1 <= n <= 50, there are 40 values of n for which the first player can force a win.
For 1 <= n <= 1 000 000, how many values of n are there for which the first player can force a win?
My Algorithm
My first step was to write a simple brute-force routine (see bruteForce) which unfortuinately can't even solve the problem for n = 50 (but n < 28 is okay).
Due to the high number of won starting positions I only printed the lost positions: 1, 5, 9, 15, 21, 25
That sequence already exists in OEIS A215721 and has a promising name: "The values of N for which the 1xN domino-covering game is a second player win".
I found a short algorithm on that website:
nv(0) = 0
nv(1) = 0
nv(N+2) = least nonnegative integer not in {nimsum(nv(k),nv(N-k)) : k <= N}
(where nimsum(a,b) is the bitwise xor of a and b). The second player wins a game iff its nim-value is 0.
→ and pretty much the same is explained here: math.stackexchange.com/questions/615242/game-involving-tiling-a-1-by-n-board-with-1-x-2-tiles
The XOR operation already solved the Nim problem 301.
I store the XOR-ed value of a board size in my mex container (name stems from the StackExchange website, same as nv() in OEIS).
In order to analyze each board with 2,3,4,...,1000000 squares I perform these steps:
- assume an empty board, no squares occupied yet
- the first move can occupy any squares such that there are empty squares on the side and right side (variables
leftandright) - I can safely assume
left <= rightfor performance reasons - lookup
mex[left]andmex[right] - XOR both values:
xored = mex[left] ^ mex[right] - set a bit for each of those XOR values in
found[xored] - then find the smallest index
ifor whichfound[i]isfalse, that means there was no XOR'ed value matching that index - and that's the result !
found as much as possible and reset only those parts that were modified.But no matter how hard I tried: the program was a bit slow and needed about 15 minutes to find the correct result.
I added a basic progress indicator and printed every 100th lost position: and all ended with a 7 !
Upon closer inspection I found that they were 680 apart each.
Then I printed every 10th lost solution and saw that they were 68 apart.
Then I printed every lost solution and needed a few second to see that a position n is lost if n - 34 was lost.
Unfortunately this pattern doesn't hold for the first 14 lost positions, therefore I hardcoded them.
See
fast() for implementation which solves the problem so fast that I can't reliably measure execution time.It keeps track of the most recent five values so that
n % 5 refers to the index where the result of n - 5 was stored.
Alternative Approaches
fast() isn't the fastest algorithm: it still needs about 30000 loop iterations for n = 10^6.
I could exploit the very repetitive nature of the algorithm and avoid them - and maybe a super-smart compiler does exactly that.
The Sprague-Grundy algorithm can be used to solve a variety of similar problems (see blog.plover.com/math/sprague-grundy.html).
Note
If I had read OEIS A215721 more carefully I would have noticed that the "n - 34" pattern was described there ... oops.
Nevertheless, I felt quite proud of myself for a moment. Worth it.
Interactive test
You can submit your own input to my program and it will be instantly processed at my server:
This is equivalent toecho 50 | ./306
Output:
Note: the original problem's input 1000000 cannot be entered
because just copying results is a soft skill reserved for idiots.
(this interactive test is still under development, computations will be aborted after one second)
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
#include <iostream> #include <vector> // uncomment to enable the slower algorithms //#define BRUTEFORCE //#define NIM_SUM
// return true if player to move wins on a board with numSquares (<= 64)
bool bruteForce(unsigned int numSquares, unsigned long long occupiedMask = 0) { // try each position and call yourself recursively for (unsigned int pos = 0; pos + 1 < numSquares; pos++) { // two neighboring bits => 11 binary => 3 const unsigned long long twoSquares = 3ULL << pos; // both bits empty ? if ((occupiedMask & twoSquares) == 0) // occupy both bits, if opponent loses then this is a winning move for the current play if (!bruteForce(numSquares, occupiedMask | twoSquares)) return true; } // all moves are losing moves return false; } // analyze all boards and count how often the first player wins
unsigned int nimSum(unsigned int maxSquares) { // https://oeis.org/A215721 // https://math.stackexchange.com/questions/615242/game-involving-tiling-a-1-by-n-board-with-1-x-2-tiles // https://blog.plover.com/math/sprague-grundy.html unsigned int numLost = 0; std::vector<unsigned int> mex(maxSquares + 1, 0); // find maximum value created by xoring states unsigned int maxXor = 1; while (maxXor < maxSquares) maxXor <<= 1; // track numbers of xored states std::vector<bool> found(maxXor, false); for (unsigned int i = 2; i <= maxSquares; i++) { // empty squares on the left and right side after the first move int left = 0; int right = i - 2; // remember the highest XOR value unsigned int lastXor = 0; while (left <= right) { auto xored = mex[left] ^ mex[right]; found[xored] = true; // remember the largest state (to speed up the clean-up/reset) if (lastXor < xored) lastXor = xored; // slide one position to the right left++; right--; } // find smallest number which was NOT create during one of the XOR steps unsigned int unused = 0; while (found[unused]) unused++; // finished computing current value mex[i] = unused; // first player only loses when mex[i] == 0 if (mex[i] == 0) { numLost++; if (numLost % 100 == 0) std::cout << i << "\t" << std::flush; } // erase all values (much faster than creating a new shiny std::vector) for (unsigned int reset = 0; reset <= lastXor; reset++) found[reset] = false; } return maxSquares - numLost; } // super-fast algorithm: implement the pattern observed in nimSum() // nextLostPosition(n) = nextLostPosition(n - 5) + 34 // except for the first 14 values { 1, 5, 9, 15, 21, 25, 29, 35, 39, 43, 55, 59, 63 }
unsigned int fast(unsigned int maxSquares) { const auto Precomputed = 13; const char Initial[Precomputed] = { 1, 5, 9, 15, 21, 25, 29, 35, 39, 43, 55, 59, 63 }; // store only the most recent 5 values unsigned int last5[5]; unsigned int numLost = 0; while (true) { // a(n) = a(n - 5) + 34 auto current = last5[numLost % 5] + 34; // except for the first 13 values if (numLost < Precomputed) current = Initial[numLost]; // found enough if (current > maxSquares) return maxSquares - numLost; // store the least recent 5 values last5[numLost % 5] = current; numLost++; } return 0; // never reached } int main() { unsigned int limit = 1000000; std::cin >> limit; // slowest algorithm #ifdef BRUTEFORCE unsigned int won = 0; for (unsigned int n = 1; n <= limit; n++) if (!bruteForce(n)) { std::cout << n << " " << std::flush; won++; } std::cout << won << std::endl; #endif // idea based on OEIS algorithm #ifdef NIM_SUM std::cout << nimSum(limit) << std::endl; #endif // my fastest algorithm std::cout << fast (limit) << std::endl; return 0; }
This solution contains 26 empty lines, 34 comments and 6 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in less than 0.01 seconds on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
September 16, 2017 submitted solution
September 16, 2017 added comments
Difficulty
Project Euler ranks this problem at 55% (out of 100%).
Links
projecteuler.net/thread=306 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
Python github.com/evilmucedin/project-euler/blob/master/euler306/euler306.py (written by Den Raskovalov)
Python github.com/LaurentMazare/ProjectEuler/blob/master/e306.py (written by Laurent Mazare)
Python github.com/Meng-Gen/ProjectEuler/blob/master/306.py (written by Meng-Gen Tsai)
Python github.com/smacke/project-euler/blob/master/python/306.py (written by Stephen Macke)
C++ github.com/roosephu/project-euler/blob/master/306.cpp (written by Yuping Luo)
Perl github.com/shlomif/project-euler/blob/master/project-euler/306/euler-306-v1.pl (written by Shlomi Fish)
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 304 - Primonacci |

|
Chip Defects - problem 307 >> |