| << problem 84 - Monopoly odds |

|
Cuboid route - problem 86 >> |
Problem 85: Counting rectangles
(see projecteuler.net/problem=85)
By counting carefully it can be seen that a rectangular grid measuring 3 by 2 contains eighteen rectangles:
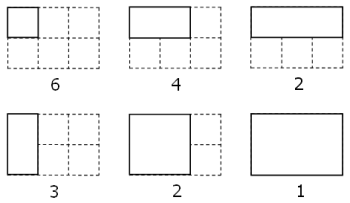
Although there exists no rectangular grid that contains exactly two million rectangles, find the area of the grid with the nearest solution.
My Algorithm
When you look at the "one-dimensional" case (an area with only 1 row):
arearectanglestotal
1x111
2x12+13
3x13+2+16
4x14+3+2+110
These are the triangle numbers T(x) = x * dfrac{x+1}{2}, see en.wikipedia.org/wiki/Triangular_number
The same pattern appears in the 2D case with more than 1 row.
An area A contains:
A(x,y) = T(x) * T(y) = dfrac{x(x+1)}{2} * dfrac{y(y+1)}{2}
= dfrac{1}{4} xy * (x+1)(y+1)
Under the assumption that y > x I iterate over all x and y until I find the first area exceeding the limit.
Each subsequent grid can't yield a better solution because of A(x,y+1) > A(x,y).
The grid with the nearest solution is the grid where the number of rectangles r is is closest to 2000000, i.e. where abs(r - 2000000) is minimized.
Interactive test
You can submit your own input to my program and it will be instantly processed at my server:
This is equivalent toecho "1 18" | ./85
Output:
Note: the original problem's input 2000000 cannot be entered
because just copying results is a soft skill reserved for idiots.
(this interactive test is still under development, computations will be aborted after one second)
My code
… was written in C++ and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
#include <iostream> #include <cmath> int main() { unsigned int tests = 1; std::cin >> tests; while (tests--) { unsigned int target = 2000000; std::cin >> target; // assume x <= y, therefore x <= sqrt(limit) unsigned int root = sqrt(target); unsigned int bestRectangles = 0; unsigned int bestArea = 0; for (unsigned int x = 1; x <= root + 1; x++) // allow slight overshooting { // start with a sqaure unsigned int y = x; // number of rectangles unsigned int rectangles = 0; // slowly increase y until too many rectangle in the grid do { unsigned int area = x * y; // the formula derived above rectangles = x * (x + 1) * y * (y + 1) / 4; // closer to desired number of rectangles than before ? if (abs(bestRectangles - target) > abs(rectangles - target)) { bestRectangles = rectangles; bestArea = area; } // prefer larger areas, too (additional requirement of Hackerrank) if (abs(bestRectangles - target) == abs(rectangles - target) && bestArea < area) bestArea = area; y++; } while (rectangles < target); // just a speed-up ... abortion when the inner loop exited with a square area x*y // => it means that no further solutions possible, area already too large if (y == x + 1) // plus one because y was incremented before leaving the inner loop break; } std::cout << bestArea << std::endl; } return 0; }
This solution contains 8 empty lines, 9 comments and 2 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in less than 0.01 seconds on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
March 12, 2017 submitted solution
May 8, 2017 added comments
Hackerrank
see https://www.hackerrank.com/contests/projecteuler/challenges/euler085
My code solves 15 out of 15 test cases (score: 100%)
Difficulty
Project Euler ranks this problem at 15% (out of 100%).
Hackerrank describes this problem as medium.
Note:
Hackerrank has strict execution time limits (typically 2 seconds for C++ code) and often a much wider input range than the original problem.
In my opinion, Hackerrank's modified problems are usually a lot harder to solve. As a rule thumb: brute-force is rarely an option.
Links
projecteuler.net/thread=85 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
C# www.mathblog.dk/project-euler-85-rectangles-rectangular-grid/ (written by Kristian Edlund)
C# github.com/HaochenLiu/My-Project-Euler/blob/master/085.cs (written by Haochen Liu)
Python github.com/hughdbrown/Project-Euler/blob/master/euler-085.py (written by Hugh Brown)
Python github.com/Meng-Gen/ProjectEuler/blob/master/85.py (written by Meng-Gen Tsai)
Python github.com/nayuki/Project-Euler-solutions/blob/master/python/p085.py (written by Nayuki)
C++ github.com/zmwangx/Project-Euler/blob/master/085/085.cpp (written by Zhiming Wang)
Java github.com/dcrousso/ProjectEuler/blob/master/PE085.java (written by Devin Rousso)
Java github.com/nayuki/Project-Euler-solutions/blob/master/java/p085.java (written by Nayuki)
Java github.com/thrap/project-euler/blob/master/src/Java/Problem85.java (written by Magnus Solheim Thrap)
Go github.com/frrad/project-euler/blob/master/golang/Problem085.go (written by Frederick Robinson)
Mathematica github.com/nayuki/Project-Euler-solutions/blob/master/mathematica/p085.mathematica (written by Nayuki)
Mathematica github.com/steve98654/ProjectEuler/blob/master/085.nb
Haskell github.com/nayuki/Project-Euler-solutions/blob/master/haskell/p085.hs (written by Nayuki)
Haskell github.com/roosephu/project-euler/blob/master/85.hs (written by Yuping Luo)
Clojure github.com/rm-hull/project-euler/blob/master/src/euler085.clj (written by Richard Hull)
Scala github.com/samskivert/euler-scala/blob/master/Euler085.scala (written by Michael Bayne)
Perl github.com/gustafe/projecteuler/blob/master/085-Counting-rectangles.pl (written by Gustaf Erikson)
Perl github.com/shlomif/project-euler/blob/master/project-euler/85/euler-85.pl (written by Shlomi Fish)
Rust github.com/gifnksm/ProjectEulerRust/blob/master/src/bin/p085.rs
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 84 - Monopoly odds |

|
Cuboid route - problem 86 >> |