| << problem 308 - An amazing Prime-generating Automaton |

|
Nim Square - problem 310 >> |
Problem 309: Integer Ladders
(see projecteuler.net/problem=309)
In the classic "Crossing Ladders" problem, we are given the lengths x and y of two ladders resting on the opposite walls of a narrow, level street.
We are also given the height h above the street where the two ladders cross and we are asked to find the width of the street (w).
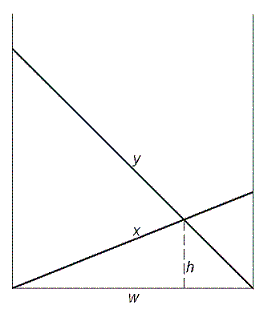
Here, we are only concerned with instances where all four variables are positive integers.
For example, if x = 70, y = 119 and h = 30, we can calculate that w = 56.
In fact, for integer values x, y, h and 0 < x < y < 200, there are only five triplets (x,y,h) producing integer solutions for w:
(70, 119, 30), (74, 182, 21), (87, 105, 35), (100, 116, 35) and (119, 175, 40).
For integer values x, y, h and 0 < x < y < 1 000 000, how many triplets (x,y,h) produce integer solutions for w?
My Algorithm
Each ladders forms two right triangles:
- the first triangle consists of the ladder x (or y), the height X (or Y) where the ladder touches the wall and the width w of the lane.
- the second triangle consists of the lower part of the ladder x_1 (or y_1), the height h where both ladders cross and a part w_1 (or w_2) of the lane.
It can be seen that
(1) w = w_1 + w_2.
The angle alpha between ladder x and the lane is part of both triangle formed by the first ladder:
(2) cos alpha = dfrac{X}{w} and cos alpha = dfrac{h}{w_1}
The same can be said about an angle beta of ladder y:
(3) cos beta = dfrac{Y}{w} and cos beta = dfrac{h}{w_2}
Both equations of (2) can be merged (and the same for (3) ):
(4) dfrac{X}{w} = dfrac{h}{w_1}
(5) dfrac{Y}{w} = dfrac{h}{w_2}
Let's transform (4) and (5), merge them and solve for w_1:
(6) w * h = X * w_1
(7) w * h = Y * w_2
(8) X * w_1 = Y * w_2
(9) w_1 = frac{Y * w_2}{X}
Combining (1) and (9):
(10) w = frac{Y * w_2}{X} + w_2
Transform (7) and substitute in (10):
(11) w = frac{Y * w_2}{h}
(12) frac{Y * w_2}{h} = frac{Y * w_2}{X} + w_2
Simplify:
(13) frac{Y * w_2}{h} = frac{Y * w_2 + X * w_2}{X}
(14) frac{Y}{h} = frac{Y + X}{X}
And solve for h:
(15) h = dfrac{Y}{frac{Y + X}{X}}
(16) h = dfrac{XY}{Y + X}
That means that I have to find the height above ground where both ladders touch the wall.
If frac{XY}{Y + X} is an integer, then I have a solution.
Wikipedia has the formula in a different notation (see en.wikipedia.org/wiki/Crossed_ladders_problem , they replaced X by A and Y by B):
dfrac{1}{X} + dfrac{1}{Y} = dfrac{1}{h}
My program generates all Pythagorean triples (see en.wikipedia.org/wiki/Pythagorean_triple , my code is based on my solution for problem 75).
A container
sides enumerates for each of the legs the length of the other leg (if c^2 = a^2 + b^2 then it stores a in sides[b] and b in sides[a]).This is done for all basic triples as well as for all multiples.
In the second phase all values of
sides[i] are compared to each other:- they are triangles where one side is equal, that's the shared width w of the lane
- the other leg is the height of the point where each ladder touches a wall
- the height h of their intersection is h = dfrac{XY}{Y + X} according to equation (16)
- and the height h is only an integer if XY is a multiple of Y + X
Note
There is probably a shorter way to derive equation (16). However, any website about the "Crossing Ladders Problem" doesn't show
how they arrive at that formula, they present it as "obviously easy". It wasn't easy for me and took quite a few attempts to get it right.
On the other hand, it's an easy task for Wolfram Alpha ... it can do all the heavy lifting (unfortunately without printing intermediate steps):
www.wolframalpha.com/input/?i=h/u=a/w and h/v=b/w and u+v=w
Interactive test
You can submit your own input to my program and it will be instantly processed at my server:
This is equivalent toecho 200 | ./309
Output:
Note: the original problem's input 1000000 cannot be entered
because just copying results is a soft skill reserved for idiots.
(this interactive test is still under development, computations will be aborted after one second)
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
#include <iostream> #include <vector> #include <algorithm> // most of the code is based on problem 75
// find greatest common divisor
template <typename T> T gcd(T a, T b) { while (a != 0) { T c = a; a = b % a; b = c; } return b; } int main() { // 10^6 unsigned int limit = 1000000; std::cin >> limit; std::vector<std::vector<unsigned int>> sides(limit); // generate all Pythagorean triples (see https://en.wikipedia.org/wiki/Pythagorean_triple ) for (unsigned int m = 2; m*m < limit; m++) for (unsigned int n = (m & 1) + 1; n < m; n += 2) { // only valid m and n if (gcd(m, n) != 1) continue; // compute basic triple auto a = m*m - n*n; auto b = 2*m*n; auto c = m*m + n*n; // and all multiples for (unsigned int k = 1; k*c < limit; k++) // longest side must be < 10^6 { // either height is shorter than width ... sides[k*a].push_back(k*b); // or the other way around sides[k*b].push_back(k*a); } } auto count = 0; // process all triangles with one identical side (the width of the street) for (const auto& current : sides) { // compare all potential heights for (size_t left = 0; left < current.size(); left++) for (size_t right = left + 1; right < current.size(); right++) { auto X = current[left]; auto Y = current[right]; // see "Algorithm" for an explanation of the formula if ((X * (unsigned long long)Y) % (X + Y) == 0) count++; // note: need 64 bit multiplication because of potential overflows } } // display result std::cout << count << std::endl; return 0; }
This solution contains 10 empty lines, 14 comments and 3 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in 0.8 seconds on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
Peak memory usage was about 59 MByte.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
July 27, 2017 submitted solution
July 27, 2017 added comments
Difficulty
Project Euler ranks this problem at 50% (out of 100%).
Links
projecteuler.net/thread=309 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
Python github.com/LaurentMazare/ProjectEuler/blob/master/e309.py (written by Laurent Mazare)
C++ github.com/roosephu/project-euler/blob/master/309.cpp (written by Yuping Luo)
Sage github.com/roosephu/project-euler/blob/master/309.sage (written by Yuping Luo)
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 308 - An amazing Prime-generating Automaton |

|
Nim Square - problem 310 >> |