| << problem 297 - Zeckendorf Representation |

|
Nim - problem 301 >> |
Problem 300: Protein folding
(see projecteuler.net/problem=300)
In a very simplified form, we can consider proteins as strings consisting of hydrophobic (H) and polar (P) elements, e.g. HHPPHHHPHHPH.
For this problem, the orientation of a protein is important; e.g. HPP is considered distinct from PPH. Thus, there are 2n distinct proteins consisting of n elements.
When one encounters these strings in nature, they are always folded in such a way that the number of H-H contact points is as large as possible, since this is energetically advantageous.
As a result, the H-elements tend to accumulate in the inner part, with the P-elements on the outside.
Natural proteins are folded in three dimensions of course, but we will only consider protein folding in two dimensions.
The figure below shows two possible ways that our example protein could be folded (H-H contact points are shown with red dots).
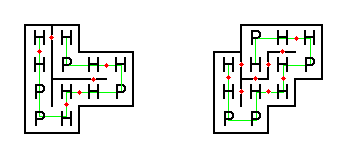
The folding on the left has only six H-H contact points, thus it would never occur naturally.
On the other hand, the folding on the right has nine H-H contact points, which is optimal for this string.
Assuming that H and P elements are equally likely to occur in any position along the string, the average number of H-H contact points in an optimal folding of a random protein string of length 8 turns out to be 850 / 28=3.3203125.
What is the average number of H-H contact points in an optimal folding of a random protein string of length 15?
Give your answer using as many decimal places as necessary for an exact result.
My Algorithm
The core idea is:
- generate all possible layouts (see
search()) - for each layout: "fill" it with all possible proteins and count contact points (see
optimize)
search() uses a 30x30 grid where the first element is placed at (15,15).Since all rotated and mirrored proteins yield the same number of contact points I also place the second element at (16,15).
In each subsequent step all possible continuations are tried until 15 elements are placed on the grid.
I decided to label those elements
a, b, ..., o (equivalent to First+0, First+1, ..., First+14). Empty cells are with a zero.When 15 elements are stored in
grid, then the function optimize finds all connections between cells.E.g. in the example image there is a contact between 0 and 14 (the first and the last element of the protein).
It deliberately ignores immediate neighbors, such as 0 and 1 because they always have a contact independent of the protein's layout.
This accelerates the analysis because those contacts of immediate neighbors can be pre-computed efficiently in
main() and reduce the time spent in optimize considerably.Several proteins share the same layout and thus have the same number of contact points.
Even more, several protein are not identical but "similar": their layout varies but they have contact points at the same locations.
My "cache" named
visited detects those identical and those similar proteins to speed up the process.The contact points are based on bit masks: if element 3 and element 7 have a contact, then the bitmask will be
(1 << 3) | (1 << 7).When I iterate over all proteins then there will be
1 << length combinations. I decided that a zero bit refers to a hydrophobic element.Thus only if
(protein & contactMask) == 0 then both elements are hydrophobic.
Note
The grid is 30x30 because when I start in the middle of the grid then a protein which is a straight line could extend to (29,15).
Obviously this layout has only contact points between immediate neighboring elements and is not an optimal choice for most proteins.
On the other hand, proteins with many contact points are often very compact.
If I don't search the whole grid for potential contact points then I could miss a few.
As it turns out, missing contacts doesn't matter for sub-optimal layout - as long as I correctly process all optimal layouts.
And it's even okay to get a few optimal layouts wrong - as long as there as multiple optimal layout and I don't mess up all of them.
I played around with the value ignoreStraight: reducing the search window to the area (9,9) - (21,21) still produces the correct result.
This is only true for proteins with 15 elements, therefore I skip this optimization for other protein lengths.
Placing the second element always at (16,15) is possible because of the massive amount of rotated and mirrored proteins.
A similar optimization is to call optimize only if the last element's y >= Center (which is 15):
For each protein which the last element at (x,y) there will be a mirrored protein ended at (x, 2*Center - y).
I tried to implement another optimization:
for each protein with a sequence abc..mno there is a flipped protein onm...bca. Thus I could skip about half of all protein sequences.
In the end I couldn't achieve a speed-up and removed the code.
I liked this problem !
Interactive test
You can submit your own input to my program and it will be instantly processed at my server:
This is equivalent toecho 8 | ./300
Output:
Note: the original problem's input 15 cannot be entered
because just copying results is a soft skill reserved for idiots.
(this interactive test is still under development, computations will be aborted after one second)
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
#include <iostream> #include <iomanip> #include <vector> #include <set> // operate on a 30x30 grid, each protein starts at (Center, Center)
const unsigned int GridSize = 30; const unsigned int Center = GridSize / 2; typedef char Grid[GridSize][GridSize]; // indicator for an empty cell
const char Empty = 0; // protein's first element is 'a', then 'b', ..., 'e'
const char First = 'a'; // optimized number of hydrophobic contacts per protein
std::vector<unsigned int> best; // number of direct contacts between immediate neighbors (minimum value, independent of folding)
std::vector<unsigned int> direct; // keep track of past contact points sequences (detect duplicates / strong similiarities)
std::set<std::vector<unsigned int>> visited; // check each protein whether the current grid is better than anything seen before
void optimize(unsigned int length, const Grid& grid) { // list of neighbors, each pair is stored as a bitmask std::vector<unsigned int> contacts; // count how many occupied cells I've seen unsigned int seen = 0; // extremely straight foldings can't be optimal because they have only contacts between directs neighbors unsigned int ignoreStraight = 9; // empirical value if (length != 15) ignoreStraight = 0; // walk through the grid for (unsigned int i = ignoreStraight; i + 1 + ignoreStraight < GridSize; i++) for (unsigned int j = ignoreStraight; j + 1 + ignoreStraight < GridSize; j++) { // already visited the entire protein ? if (seen + 1 >= length) break; // ignore empty cells if (grid[i][j] == Empty) continue; // one more element visited seen++; // get its index (0..length-1) auto from = grid[i][j] - First; // check right neighbor if (grid[i + 1][j] != Empty) { auto to = grid[i + 1][j] - First; if (from != to + 1 && from + 1 != to) contacts.push_back((1 << from) | (1 << to)); } // check bottom neighbor if (grid[i][j + 1] != Empty) { auto to = grid[i][j + 1] - First; if (from != to + 1 && from + 1 != to) contacts.push_back((1 << from) | (1 << to)); } } // no contacts at all ? (besides direct contact) if (contacts.empty()) return; // already had a similar folding ? (same contact points) if (visited.count(contacts) != 0) return; visited.insert(contacts); // for each protein check whether more hydrophobic contacts exist auto numProteins = 1 << length; for (auto protein = 0; protein < numProteins; protein++) { // at least all direct contacts auto found = direct[protein]; // can't beat the previous record ? if (found + contacts.size() <= best[protein]) continue; // count other contact points for (auto contactMask : contacts) { // are both neighbors hydrophobic ? if ((protein & contactMask) == 0) found++; } // better than before ? if (best[protein] < found) best[protein] = found; } } // generate recursive all possible layouts
void search(unsigned int current, unsigned int length, Grid& grid, unsigned int x, unsigned int y) { // protein completely placed on grid ? if (current == length) { // don't check layouts mirrored along y-axis if (y >= Center) optimize(length, grid); // done return; } // try all possible continuations // go left if (grid[x - 1][y] == Empty) { grid[x - 1][y] = current + First; search(current + 1, length, grid, x - 1, y); grid[x - 1][y] = Empty; } // go right if (grid[x + 1][y] == Empty) { grid[x + 1][y] = current + First; search(current + 1, length, grid, x + 1, y); grid[x + 1][y] = Empty; } // go down if (grid[x][y - 1] == Empty) { grid[x][y - 1] = current + First; search(current + 1, length, grid, x, y - 1); grid[x][y - 1] = Empty; } // go up if (grid[x][y + 1] == Empty) { grid[x][y + 1] = current + First; search(current + 1, length, grid, x, y + 1); grid[x][y + 1] = Empty; } } int main() { unsigned int length = 15; std::cin >> length; // allocate memory auto numProteins = 1 << length; direct.resize(numProteins, 0); best .resize(numProteins, 0); // count direct neighboring hydrophobic elements in each protein for (auto protein = 0; protein < numProteins; protein++) { for (unsigned int i = 0; i < length - 1; i++) if ((protein & (3 << i)) == 0) // 3 => bitmask of two bits direct[protein]++; best[protein] = direct[protein]; } // create an empty grid Grid grid; for (unsigned int x = 0; x < GridSize; x++) for (unsigned int y = 0; y < GridSize; y++) grid[x][y] = Empty; // always start in the middle unsigned int x = Center; unsigned int y = Center; grid[x][y] = First; // due to symmetries I can also place the second element x++; grid[x][y] = First + 1; // generate all layouts and then call optimize() search(2, length, grid, x, y); // count optimized contact points unsigned int sum = 0; for (auto x : best) sum += x; // display average std::cout << std::setprecision(14) << sum / double(best.size()) << std::endl; return 0; }
This solution contains 30 empty lines, 42 comments and 4 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in 2.6 seconds on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
Peak memory usage was about 5 MByte.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
August 27, 2017 submitted solution
August 27, 2017 added comments
Difficulty
Project Euler ranks this problem at 50% (out of 100%).
Links
projecteuler.net/thread=300 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
Python github.com/Meng-Gen/ProjectEuler/blob/master/300.py (written by Meng-Gen Tsai)
C++ github.com/evilmucedin/project-euler/blob/master/euler300/euler300.cpp (written by Den Raskovalov)
C++ github.com/roosephu/project-euler/blob/master/300.cpp (written by Yuping Luo)
Go github.com/frrad/project-euler/blob/master/golang/Problem300.go (written by Frederick Robinson)
ML github.com/LaurentMazare/ProjectEuler/blob/master/e300.ml (written by Laurent Mazare)
Sage github.com/roosephu/project-euler/blob/master/300.sage (written by Yuping Luo)
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 297 - Zeckendorf Representation |

|
Nim - problem 301 >> |