| << problem 324 - Building a tower |

|
Prime Frog - problem 329 >> |
Problem 327: Rooms of Doom
(see projecteuler.net/problem=327)
A series of three rooms are connected to each other by automatic doors.
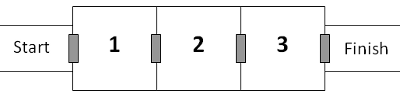
Each door is operated by a security card. Once you enter a room the door automatically closes and that security card cannot be used again.
A machine at the start will dispense an unlimited number of cards, but each room (including the starting room) contains scanners
and if they detect that you are holding more than three security cards or if they detect an unattended security card on the floor,
then all the doors will become permanently locked.
However, each room contains a box where you may safely store any number of security cards for use at a later stage.
If you simply tried to travel through the rooms one at a time then as you entered room 3 you would have used all three cards and would be trapped in that room forever!
However, if you make use of the storage boxes, then escape is possible. For example, you could enter room 1 using your first card,
place one card in the storage box, and use your third card to exit the room back to the start.
Then after collecting three more cards from the dispensing machine you could use one to enter room 1 and collect the card you placed in the box a moment ago.
You now have three cards again and will be able to travel through the remaining three doors.
This method allows you to travel through all three rooms using six security cards in total.
It is possible to travel through six rooms using a total of 123 security cards while carrying a maximum of 3 cards.
Let C be the maximum number of cards which can be carried at any time.
Let R be the number of rooms to travel through.
Let M(C,R) be the minimum number of cards required from the dispensing machine to travel through R rooms carrying up to a maximum of C cards at any time.
For example, M(3,6)=123 and M(4,6)=23.
And, sum{M(C,6)}=146 for 3 <= C <= 4.
You are given that sum{M(C,10)}=10382 for 3 <= C <= 10.
Find sum{M(C,30)} for 3 <= C <= 40.
My Algorithm
I process all rooms from the right to the left side. In each room I calculate the number of cards needed to escape.
Only one card is required in the right-most room: just insert it into the scanner - done.
I need two cards in the room left to the right-most room: one card to enter the last room and another card to escape.
Similarly, I need three cards in the room before that room.
Let's assume there are only three rooms - the problem statement gives away that a total of six cards are needed.
And further assume that in front of the first room is room "zero".
To exit the maze I need three cards when I'm inside the first room.
However, I cannot hold more than three cards at the same time and already needed one card to enter the first room.
So I need a few extra moves: go back to room zero, takes as many cards as possible, enter room one, deposit as many as possible and go back to room room.
These extra moves "transport" cards: I can transport C - (1+1) cards from the previous to the current room with one extra move:
one card is needed to enter the current room and another to leave the current room.
In order to have three cards available in the first room, the following sequence needs to be followed:
- take 3 cards from the dispenser in room zero
- enter room one: I have two cards left, one will be stored, the second is needed to return to room zero
- take 3 cards from the dispenser in room zero
- enter room one: I have two cards left plus one card in the storage for a total of three cards
- enter room two: I have two cards left
- enter room three: I have one cards left and that's enough to open the final door
So my algorithm is as follows:
- start with the right-most room, I need one card to exit it,
need = 1 - in the room its left side I need enough cards to enter the next room and enough cards to exit the maze from that room, too:
need += 1 - if
need > Cthen extra moves to the previous room (its left-side room) are required in order to getneedcards into the current rooms - each extra move provides
C - 2cards but increases the number ofconsumedcards byC
while loop finds the correct result if C >= 4 almost instantly (disable #define FAST).However, the results for C = 3 are enormous and that loop would take a long time to finish.
Each iteration of the simple
while loop does the same job: adding as subtracting constants.So my
#define FAST just calculates the number of iterations and finishes in less than 0.01 seconds.
Interactive test
You can submit your own input to my program and it will be instantly processed at my server:
This is equivalent toecho "10 10" | ./327
Output:
Note: the original problem's input 30 40 cannot be entered
because just copying results is a soft skill reserved for idiots.
(this interactive test is still under development, computations will be aborted after one second)
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
#include <iostream> unsigned long long search(unsigned int cards, unsigned int rooms) { // need one card to exit the right-most room unsigned long long need = 1; // I need one card to enter the next room and one to come back, thus I can transport "cards - 2" to the next room in one step const auto Transport = cards - (1 + 1); // these 2 cards are "wasted" // compute in each room how many cards I need to exit, beginning with the right-most room for (auto currentRoom = rooms; currentRoom > 0; currentRoom--) { // how many cards are required to satisfy "need", including cards wasted moving forth and back auto consumed = 0ULL; #define FAST #ifdef FAST // all iterations of the following "while"-loop are basically the same, let's process them quickly if (need >= cards) { // determine number of iterations auto moves = (need - cards) / Transport; // do I need one more to ensure need < cards at the end ? if (need - moves * Transport >= cards) moves++; // compute all iterations at once need -= moves * Transport; consumed += moves * cards; } #else // the basic algorithm becomes slow if needing many cards and Transport is small while (need >= cards) { need -= Transport; consumed += cards; } #endif // carry the remaining cards in the last move, including a card to enter the next room auto previous = need + consumed + 1; // ... and continue with the previous room (the one on the left side of the current room) need = previous; } return need; } int main() { unsigned int rooms = 30; unsigned int cards = 40; std::cin >> rooms >> cards; unsigned long long result = 0; for (unsigned int i = 3; i <= cards; i++) result += search(i, rooms); std::cout << result << std::endl; return 0; }
This solution contains 11 empty lines, 11 comments and 5 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in less than 0.01 seconds on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
October 27, 2017 submitted solution
October 27, 2017 added comments
Difficulty
Project Euler ranks this problem at 40% (out of 100%).
Links
projecteuler.net/thread=327 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
Python blog.dreamshire.com/project-euler-327/
Python github.com/evilmucedin/project-euler/blob/master/euler327/euler327.py (written by Den Raskovalov)
Python github.com/LaurentMazare/ProjectEuler/blob/master/e327.py (written by Laurent Mazare)
Python github.com/Meng-Gen/ProjectEuler/blob/master/327.py (written by Meng-Gen Tsai)
Python github.com/smacke/project-euler/blob/master/python/327.py (written by Stephen Macke)
C++ github.com/roosephu/project-euler/blob/master/327.cpp (written by Yuping Luo)
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 324 - Building a tower |

|
Prime Frog - problem 329 >> |