| << problem 146 - Investigating a Prime Pattern |

|
Exploring Pascal's triangle - problem 148 >> |
Problem 147: Rectangles in cross-hatched grids
(see projecteuler.net/problem=147)
In a 3x2 cross-hatched grid, a total of 37 different rectangles could be situated within that grid as indicated in the sketch.
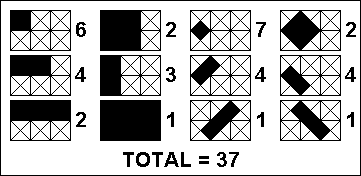
There are 5 grids smaller than 3x2, vertical and horizontal dimensions being important, i.e. 1x1, 2x1, 3x1, 1x2 and 2x2.
If each of them is cross-hatched, the following number of different rectangles could be situated within those smaller grids:
1x1: 1
2x1: 4
3x1: 8
1x2: 4
2x2: 18
Adding those to the 37 of the 3x2 grid, a total of 72 different rectangles could be situated within 3x2 and smaller grids.
How many different rectangles could be situated within 47x43 and smaller grids?
My Algorithm
The number of upright rectangles can be computed using the formulas found in problem 85:
n = T(width) * T(height) where T is the triangle number T(x) = dfrac{x(x+1)}{2}
A 3x2 grid contains dfrac{3(3+1)}{2} * dfrac{2(2+1)}{2} = dfrac{12}{2} * dfrac{6}{2} = 18 upright rectangles.
I didn't find such a nice formula for the diagonal rectangles. Fortunately brute-force counting can solve this problem in less than a second.
There are two kinds of diagonal squares:
- some have a center (x,y) that is crosses by a vertical line → x is an integer and y is an integer plus 0.5
- some have a center (x,y) that is crosses by a horizontal line → y is an integer and x is an integer plus 0.5
Its lower-right neighbor's center is at (x + 0.5, y - 0.5).
All centers have the properties 0 < x < width and 0 < y < height.
Those floating-point computations tend to be a bit slow therefore I multiplied all values by 2 and returned to integer arithmetic.
I can count all diagonal rectangles if I start at every diagonal square and find all its upper-right neighbors. This gives me all rectangles that are one unit high.
Then I go one step to the lower-right and again find all upper-right neighbors. This gives me all rectangles that are two units high.
This algorithm is repeated until there is no valid lower-right neighbor.
The variable
paritydetermines whether the first squares center is crossed by a vertical or horizontal line.
Modifications by HackerRank
Several grids have to be analyzed at once. Since all have to process smaller grids like (1,1), (1,2), (2,1), etc. I added a simple cache.
I fail two test cases because they apparantly require you to find the closed form - my simple brute-force strategy times out.
Note
Swapping the values for width and height doesn't affect the result. My algorithm is slightly faster when width > height.
Interactive test
You can submit your own input to my program and it will be instantly processed at my server:
This is equivalent toecho "1 3 2" | ./147
Output:
Note: the original problem's input 47 43 cannot be entered
because just copying results is a soft skill reserved for idiots.
(this interactive test is still under development, computations will be aborted after one second)
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
The code contains #ifdefs to switch between the original problem and the Hackerrank version.
Enable #ifdef ORIGINAL to produce the result for the original problem (default setting for most problems).
#include <iostream> #include <map> #define ORIGINAL // Hackerrank only
const unsigned int Modulo = 1000000007; // return number of different rectangles in a x*y grid (without diagonal rectangles)
unsigned int grid(unsigned int width, unsigned int height) { // triangular number, see https://en.wikipedia.org/wiki/Triangular_number // return T(width) * T(height) return (width * (width + 1) / 2) * (height * (height + 1) / 2); } // return number of different diagonal rectangles in a x*y grid
unsigned int diagonal(unsigned int width, unsigned int height) { // memoize static std::map<std::pair<unsigned int, unsigned int>, unsigned int> cache; auto id = std::make_pair(width, height); auto lookup = cache.find(id); if (lookup != cache.end()) return lookup->second; // a is the length of the longer side and b the shorter side auto a = width; auto b = height; if (a < b) std::swap(a, b); // no clever formulas, just stupid counting ... unsigned int count = 0; // for each lattice point (x,y) I can find two nearby square centers: // at (x + 0.5, y) and at (x, y + 0.5) // floating-point arithmetic was a bit slow therefore I switched to integer arithmetic: // all coordinates are multiplied by 2 for (unsigned int i = 0; i < a; i++) for (unsigned int j = 0; j < b; j++) for (unsigned int parity = 0; parity <= 1; parity++) { // left-most corner (if rotated by 45 degrees it would be the lower-left corner) auto startX = 2*i + 1 + parity; auto startY = 2*j + 2 - parity; // now try to find all possible upper-right corners of that triangle // found all rectangles started at (startX, startY) ? bool stop = false; // limit height of each rectangle auto maxHeight = 999999999; // scan along the (rotated) x-axis for (auto currentWidth = 0; !stop; currentWidth++) { // generate coordinates in a non-rotated coordinate system (still multiplied by 2) auto currentX = startX + currentWidth; auto currentY = startY - currentWidth; // out of bounds ? if (currentY <= 0) break; // scan along the (rotated) y-axis // note: not higher than any rectangle before (with the same starting point) for (auto currentHeight = 0; currentHeight < maxHeight; currentHeight++) { // upper-right corner of the current rectangle auto endX = currentX + currentHeight; auto endY = currentY + currentHeight; if (endX >= 2*a || endY >= 2*b) { // no other rectangle may be higher if (maxHeight > currentHeight) maxHeight = currentHeight; // reached right-most part ? => done stop = (currentHeight == 0); break; } // found one more rectangle count++; } } } // Hackerrank only #ifndef ORIGINAL count %= Modulo; #endif cache[id] = count; return count; } int main() { unsigned int tests = 1; std::cin >> tests; while (tests--) { unsigned int maxWidth = 47; unsigned int maxHeight = 43; std::cin >> maxWidth >> maxHeight; // count all upright and all diagonal rectangles unsigned long long sumUpright = 0; unsigned long long sumDiagonal = 0; for (unsigned int width = 1; width <= maxWidth; width++) for (unsigned int height = 1; height <= maxHeight; height++) { sumUpright += grid (width, height); sumDiagonal += diagonal(width, height); } // display result #ifdef ORIGINAL std::cout << sumUpright + sumDiagonal << std::endl; #else std::cout << sumUpright % Modulo << " " << sumDiagonal % Modulo << std::endl; #endif } return 0; }
This solution contains 18 empty lines, 28 comments and 8 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in 0.6 seconds on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
August 9, 2017 submitted solution
August 9, 2017 added comments
Hackerrank
see https://www.hackerrank.com/contests/projecteuler/challenges/euler147
My code solves 3 out of 5 test cases (score: 50%)
I failed 0 test cases due to wrong answers and 2 because of timeouts
Difficulty
Project Euler ranks this problem at 65% (out of 100%).
Hackerrank describes this problem as hard.
Note:
Hackerrank has strict execution time limits (typically 2 seconds for C++ code) and often a much wider input range than the original problem.
In my opinion, Hackerrank's modified problems are usually a lot harder to solve. As a rule thumb: brute-force is rarely an option.
Links
projecteuler.net/thread=147 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
Python blog.dreamshire.com/project-euler-147/
Python github.com/Meng-Gen/ProjectEuler/blob/master/147.py (written by Meng-Gen Tsai)
Python github.com/smacke/project-euler/blob/master/python/147.py (written by Stephen Macke)
C++ github.com/roosephu/project-euler/blob/master/147.cpp (written by Yuping Luo)
C++ github.com/steve98654/ProjectEuler/blob/master/147.cpp
Java github.com/HaochenLiu/My-Project-Euler/blob/master/147.java (written by Haochen Liu)
Java github.com/thrap/project-euler/blob/master/src/Java/Problem147.java (written by Magnus Solheim Thrap)
Go github.com/frrad/project-euler/blob/master/golang/Problem147.go (written by Frederick Robinson)
Perl github.com/shlomif/project-euler/blob/master/project-euler/147/euler-147.pl (written by Shlomi Fish)
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 146 - Investigating a Prime Pattern |

|
Exploring Pascal's triangle - problem 148 >> |