| << problem 581 - 47-smooth triangular numbers |

|
Divisibility streaks - problem 601 >> |
Problem 587: Concave triangle
(see projecteuler.net/problem=587)
A square is drawn around a circle as shown in the diagram below on the left.
We shall call the blue shaded region the L-section.
A line is drawn from the bottom left of the square to the top right as shown in the diagram on the right.
We shall call the orange shaded region a concave triangle.
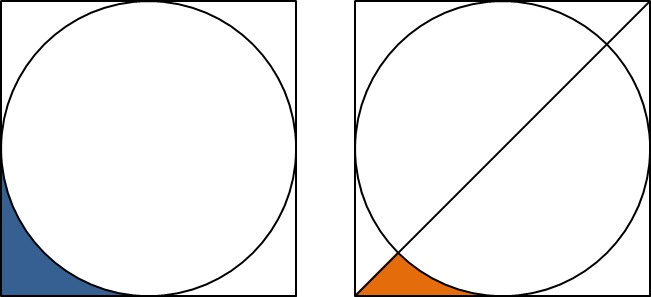
It should be clear that the concave triangle occupies exactly half of the L-section.
Two circles are placed next to each other horizontally, a rectangle is drawn around both circles, and a line is drawn from the bottom left to the top right as shown in the diagram below.
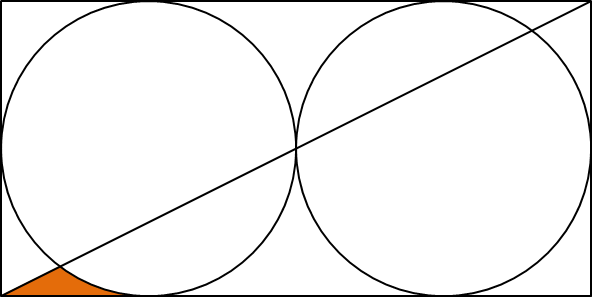
This time the concave triangle occupies approximately 36.46% of the L-section.
If n circles are placed next to each other horizontally, a rectangle is drawn around the n circles, and a line is drawn from the bottom left to the top right, then it can be shown that the least value of n for which the concave triangle occupies less than 10% of the L-section is n = 15.
What is the least value of n for which the concave triangle occupies less than 0.1% of the L-section?
My Algorithm
This is a so-called paper'n'pen problem because you can solve it without a computer.
But I like computers so much that I decided to write a proper program that solves this problem by throwing CPU cycles at it !
A little mathematics is still required:
- the line from the lower left corner to the upper right corner has the equation y = mx where m is the slope
- I define that my circles have a radius r = 1
- so that the box has a height of r+r = 2
There are four L-shaped areas between circle and box - all have the same size, so that one L-shaped area covers an area of
(1) (4 - pi) / 4 approx 0.2146
To find the intersection between the line and the first circle - which is centered at (1,1) - I solve both equation for y:
(2) y = mx
(3) (x - 1)^2 + (y - 1)^2 = 1
(4) (y - 1)^2 = 1 - (x - 1)^2
(5) y - 1 = \pm sqrt{1 - (x - 1)^2}
(6) y = 1 - sqrt{1 - (x - 1)^2} ← I only need the lower half of the circle where the first intersection takes place
The intersection is at (2) = (6):
(7) mx = 1 - sqrt{1 - (x - 1)^2}
And that's when I decided to write a "true" IT solution and solve equation (7) numerically:
- compute left and right side of equation (7)
- if they are "close enough", then abort
- else move x accordingly
- start with large moves and then make smaller moves
- see
getIntersection()(whereslopeism)
- function
getAreaL()computes the area of the L-shaped area given aslope - left of the intersection point is a triangle with area x * y / 2 = x * m x / 2
- right of the intersection point is the integral of equation (6)
- my numerical integration takes 100000 steps between the intersection point and x = 1
It took a little more than one second to find the correct solution.
Knowing that the area is strictly decreasing I re-wrote my code to work similar to binary intersection:
check only every 64th number: 64, 128, 192, ... circles and when the area is below the limit then go back and check every 32nd, then 16th, ... until
step = 1.Now the result is printed after less than 0.1 seconds.
Alternative Approaches
As I told you before, you can solve this with pen'n'paper (or Wolfram Alpha).
Note
Of course there are a few assumptions which are not always true:
- maybe
Epsilonis too large and the result will be wrong - maybe I need more than 100000 steps to accurately evaluate
getAreaL
I had fun writing this solution - for whatever reason I like numerical approaches such as Monte-Carlo simulations.
Interactive test
You can submit your own input to my program and it will be instantly processed at my server:
This is equivalent toecho 10 | ./587
Output:
Note: the original problem's input 0.1 cannot be entered
because just copying results is a soft skill reserved for idiots.
(this interactive test is still under development, computations will be aborted after one second)
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
#include <iostream> #include <cmath> const auto Epsilon = 0.00000000001; const auto NoLine = 0; // return x where line and first circle intersection
double getIntersection(double slope) { // circle: (x-1)^2 + (y-1)^2 = 1 // (y-1)^2 = 1 - (x-1)^2 // y-1 = sqrt(1 - (x-1)^2) // y = 1 - sqrt(1 - (x-1)^2) // line: y = mx <= where m is the slope // their intersection: mx = 1 - sqrt(1 - (x-1)^2) // I entered those formula in Wolfram Alpha and didn't like the output ... so let's solve this numerically ! // choose any x in 0 < x < 1 auto x = 0.5; // adjust x by this value if not precise enough auto step = 0.1; while (true) { // good enough ? auto leftSide = slope * x; auto rightSide = 1 - sqrt(1 - (x - 1)*(x - 1)); // see above how I got this formula if (fabs(leftSide - rightSide) < Epsilon) return x; // move x if (leftSide > rightSide) x -= step; else x += step; // take smaller steps step *= 0.99; } } // return area of the L-shaped area
double getAreaL(double slope) { // x-coordinate of first intersection between line and circle double intersection = 0; // area of the triangle on the left side of the intersection double leftArea = 0; if (slope > 0) { intersection = getIntersection(slope); leftArea = intersection * (intersection * slope) / 2; } // the area on the right side of the intersection can be computed exactly - but I hate ugly looking formulas and prefer C++ code :-) // numerically integrate area between intersection and "where the first circle touches the box" auto rightArea = 0.0; auto Step = (1 - intersection) / 100000; for (double x = intersection; x < 1; x += Step) { double y = 1 - sqrt(1 - (x - 1)*(x - 1)); // same formula as in getIntersection rightArea += y * Step; } return leftArea + rightArea; } int main() { // stop if below 0.1% auto limit = 0.1; std::cin >> limit; // a circle has an area of A=pi * r^2 // r=1 => A = pi // the box around the circle has an area of 2^2 = 4 // there are four L's between circle and box, I only need the one in the lower half // L = (4 - pi) / 4 = 0.21460183660255169038433915418012... auto L = getAreaL(NoLine); // NoLine=0 is a special case in getAreaL auto numCircles = 1; auto step = 64; // powers of two are great, but could be any other positive number, too (even 1) while (true) { auto slope = 1.0 / numCircles; auto area = getAreaL(slope); // area small enough ? auto percentage = 100 * area / L; if (percentage < limit) { // reached small step size, found solution if (step == 1) break; // maybe I "jumped over" the correct solution, go back and reduce step size numCircles -= step; step /= 2; } // look at next slope numCircles += step; } // and print the solution std::cout << numCircles << std::endl; return 0; }
This solution contains 16 empty lines, 29 comments and 2 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in 0.04 seconds on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
October 23, 2017 submitted solution
October 23, 2017 added comments
Difficulty
Project Euler ranks this problem at 20% (out of 100%).
Links
projecteuler.net/thread=587 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
Python github.com/Meng-Gen/ProjectEuler/blob/master/587.py (written by Meng-Gen Tsai)
Python github.com/nayuki/Project-Euler-solutions/blob/master/python/p587.py (written by Nayuki)
C++ github.com/evilmucedin/project-euler/blob/master/euler587/587.cpp (written by Den Raskovalov)
C++ github.com/roosephu/project-euler/blob/master/587.cpp (written by Yuping Luo)
Java github.com/nayuki/Project-Euler-solutions/blob/master/java/p587.java (written by Nayuki)
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 581 - 47-smooth triangular numbers |

|
Divisibility streaks - problem 601 >> |