| << problem 108 - Diophantine reciprocals I |

|
Diophantine reciprocals II - problem 110 >> |
Problem 109: Darts
(see projecteuler.net/problem=109)
In the game of darts a player throws three darts at a target board which is split into twenty equal sized sections numbered one to twenty.
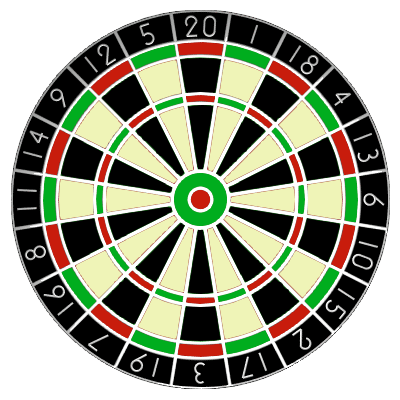
The score of a dart is determined by the number of the region that the dart lands in. A dart landing outside the red/green outer ring scores zero.
The black and cream regions inside this ring represent single scores. However, the red/green outer ring and middle ring score double and treble scores respectively.
At the centre of the board are two concentric circles called the bull region, or bulls-eye. The outer bull is worth 25 points and the inner bull is a double, worth 50 points.
There are many variations of rules but in the most popular game the players will begin with a score 301 or 501 and the first player to reduce their running total to zero is a winner.
However, it is normal to play a "doubles out" system, which means that the player must land a double (including the double bulls-eye at the centre of the board) on their final dart to win;
any other dart that would reduce their running total to one or lower means the score for that set of three darts is "bust".
When a player is able to finish on their current score it is called a "checkout" and the highest checkout is 170: T20 T20 D25 (two treble 20s and double bull).
There are exactly eleven distinct ways to checkout on a score of 6:
D3
D1D2
S2D2
D2D1
S4D1
S1S1D2
S1T1D1
S1S3D1
D1D1D1
D1S2D1
S2S2D1
Note that D1 D2 is considered different to D2 D1 as they finish on different doubles. However, the combination S1 T1 D1 is considered the same as T1 S1 D1.
In addition we shall not include misses in considering combinations; for example, D3 is the same as 0 D3 and 0 0 D3.
Incredibly there are 42336 distinct ways of checking out in total.
How many distinct ways can a player checkout with a score less than 100?
My Algorithm
Each field of the board is represented by a simple struct Field.
It carries information about the base value (e.g. 20), the factor (single, double, triple) and the total score of this field (e.g. 20 with factor 3 → 60).
All fields are added to a container fields. I even include a "zero" field which indicates a dart that missed the board. It has value = factor = zero.
The outer loop iterates over all total scores 1 to 99.
Three inner loops iterate over all fields: I start with the third dart which must be a double (I only did this make the code run faster).
The first and second dart are interchangeable, therefore I define that the field ID of the second dart can't be lower than the first dart.
If the sum of all three dart matches the total score then a valid checkout was achieved.
The misses can only occur on the first dart or the first plus the second dart. Therefore the "zero" field must be the first in my list of fields.
Alternative Approaches
I'm pretty sure you can find some closed formula. But my brute-force approach finishes in less than 0.01 seconds, even for the full board (lessPointsThan = 181) ...
Note
You can optimize the loops, too: if you sort ascendingly the fields by their total value then some continue statements can be replaced by break.
Interactive test
You can submit your own input to my program and it will be instantly processed at my server:
This is equivalent toecho 181 | ./109
Output:
Note: the original problem's input 100 cannot be entered
because just copying results is a soft skill reserved for idiots.
(this interactive test is still under development, computations will be aborted after one second)
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
#include <iostream> #include <vector> // a single field
struct Field { Field(unsigned int value_, unsigned int factor_) : value(value_), factor(factor_), total(value_ * factor_) {} unsigned int value; unsigned int factor; unsigned int total; }; int main() { unsigned int lessPointsThan = 100; std::cin >> lessPointsThan; // set up board std::vector<Field> fields; // dummy element: dart missed the board fields.push_back({ 0, 0 }); // "normal" fields incl. double and triple ring for (unsigned int i = 1; i <= 20; i++) { fields.push_back({ i, 1 }); fields.push_back({ i, 2 }); fields.push_back({ i, 3 }); } // bull's eye fields.push_back({ 25, 1 }); fields.push_back({ 25, 2 }); // final result unsigned int combinations = 0; // count combinations when 1..99 points left on the board for (unsigned int total = 1; total < lessPointsThan; total++) { // start with the final dart because its restrictions eliminate many iterations ... for (auto third : fields) { // must be double if (third.factor != 2 || third.total > total) // simple tweak: if this dart scores too many points then skip it continue; // throw first and second dart for (size_t dart1 = 0; dart1 < fields.size(); dart1++) for (size_t dart2 = dart1; dart2 < fields.size(); dart2++) { auto first = fields[dart1]; auto second = fields[dart2]; // correct number of points ? auto sum = first.total + second.total + third.total; if (sum != total) continue; // yes, one more solution combinations++; } } } std::cout << combinations << std::endl; return 0; }
This solution contains 10 empty lines, 12 comments and 2 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in less than 0.01 seconds on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
May 17, 2017 submitted solution
May 17, 2017 added comments
Difficulty
Project Euler ranks this problem at 45% (out of 100%).
Links
projecteuler.net/thread=109 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
C# www.mathblog.dk/project-euler-109-checkout-darts/ (written by Kristian Edlund)
C# github.com/HaochenLiu/My-Project-Euler/blob/master/109.cs (written by Haochen Liu)
Python github.com/LaurentMazare/ProjectEuler/blob/master/e109.py (written by Laurent Mazare)
Python github.com/Meng-Gen/ProjectEuler/blob/master/109.py (written by Meng-Gen Tsai)
Python github.com/nayuki/Project-Euler-solutions/blob/master/python/p109.py (written by Nayuki)
Python github.com/roosephu/project-euler/blob/master/109.py (written by Yuping Luo)
Python github.com/smacke/project-euler/blob/master/python/109.py (written by Stephen Macke)
C++ github.com/zmwangx/Project-Euler/blob/master/109/109.cpp (written by Zhiming Wang)
Java github.com/dcrousso/ProjectEuler/blob/master/PE109.java (written by Devin Rousso)
Java github.com/nayuki/Project-Euler-solutions/blob/master/java/p109.java (written by Nayuki)
Java github.com/thrap/project-euler/blob/master/src/Java/Problem109.java (written by Magnus Solheim Thrap)
Go github.com/frrad/project-euler/blob/master/golang/Problem109.go (written by Frederick Robinson)
Mathematica github.com/nayuki/Project-Euler-solutions/blob/master/mathematica/p109.mathematica (written by Nayuki)
Mathematica github.com/steve98654/ProjectEuler/blob/master/109.nb
Scala github.com/samskivert/euler-scala/blob/master/Euler109.scala (written by Michael Bayne)
Perl github.com/shlomif/project-euler/blob/master/project-euler/109/euler-109.pl (written by Shlomi Fish)
Rust github.com/gifnksm/ProjectEulerRust/blob/master/src/bin/p109.rs
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 | 807 | 808 | 809 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 108 - Diophantine reciprocals I |

|
Diophantine reciprocals II - problem 110 >> |