| << problem 125 - Palindromic sums |

|
abc-hits - problem 127 >> |
Problem 126: Cuboid layers
(see projecteuler.net/problem=126)
The minimum number of cubes to cover every visible face on a cuboid measuring 3 x 2 x 1 is twenty-two.
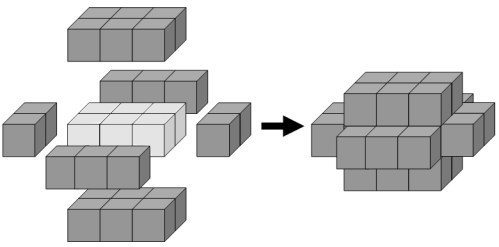
If we then add a second layer to this solid it would require forty-six cubes to cover every visible face,
the third layer would require seventy-eight cubes, and the fourth layer would require one-hundred and eighteen cubes to cover every visible face.
However, the first layer on a cuboid measuring 5 x 1 x 1 also requires twenty-two cubes; similarly the first layer on cuboids measuring 5 x 3 x 1, 7 x 2 x 1, and 11 x 1 x 1 all contain forty-six cubes.
We shall define C(n) to represent the number of cuboids that contain n cubes in one of its layers. So C(22) = 2, C(46) = 4, C(78) = 5, and C(118) = 8.
It turns out that 154 is the least value of n for which C(n) = 10.
Find the least value of n for which C(n) = 1000.
My Algorithm
The initial cuboid (without any layers) has six sides:
- front and back side, both with an area of width * height
- left and right side, both with an area of height * depth
- top and bottom side, both with an area of depth * width
Each part of the surface is covered by the first layer. That means:
C(1) = 2 * (width * height + height * depth + depth * width).
For the 3 x 2 x 1 cuboid: C(1) = 2 * (3 * 2 + 2 * 1 + 1 * 3) = 2 * (6 + 2 + 3) = 2 * 11 = 22
The computation of the second, third, fourth, ... layer wasn't obvious to me. My drawing skills are sub-par at best.
So I decided to write some code: start with a shape and move that shape one unit left, right, up, down, forward and backward
(start each move at the initial position). The difference between the old shape and the shape created by these six movements is the volume of the new layer.
My function
naive() (last lines of my code) performs exactly these steps. Starting with a specified cuboid it finds the volume of each additional layer and prints it.Playing around with several cuboid sizes I saw a pattern:
C(2) = C(1) + 4 * (width + height + depth)
C(3) = C(2) + 4 * (width + height + depth) + 8
C(4) = C(3) + 4 * (width + height + depth) + 16
C(5) = C(4) + 4 * (width + height + depth) + 24
A bit more general:
C(1) = 2 * (width * height + height * depth + depth * width).
C(n) = C(n-1) + 4 * (width + height + depth) + 8 * (n - 2)
You can convert the second formula into a closed form but then the equation looks a bit messy.
The C++ compiler won't generate much faster code, too. The function
Cuboid::calculate evaluates these two equations.In order to solve C(n) = x for arbitrary x (it's x = 1000 in the original problem) I wrote code based on
std::map:- each cuboids is represented by
Cuboid, it stores the size of the initial cuboid and the number of layers Cuboidcan be sorted by the size of the outermost layer (and then by it's sides)- since
std::mapis an ascendingly sorted container, it's first element is the cuboid with the smallest outermost layer
- pick and remove the first (= smallest) cuboid from the container
- add a cuboid with
width + 1to the container - add another cuboid with
height + 1 - and a cuboid with
depth + 1 - finally add a cuboid with
layer + 1to that container
add() function. It rejects cuboids where height > width and depth > height to avoidhaving the same (rotated) cuboid multiple times in the container. Adding exactly the same container twice is prevented, too.
On top of that,
add() keeps track of the volume of the most recent layer (in count[]).That algorithm stops when the smallest cuboid has exactly 1000 "siblings" (→ the
count of the current volume is 1000).It shows the correct result after about 4 seconds.
However, my profiler showed that a few million cuboids where added (and removed) from the container.
The overhead of memory allocation was responsible for the majority of the execution time.
A much faster approach is to guess an upper limit of the result and then create all cuboids (and layers) that fit into that limit.
Keeping track of just the various values of C() instead of the cuboids can be done with a small
std::vector.The program becomes about 50x faster and has almost no memory consumption. See my function
fast().The main problem is to find a good guess for the upper limit.
fast() returns 0 if no result was found, that's when the initial guess has to be incremented and another call to fast() is required.Starting with a very high guess will find the result but might waste lots of time computing cuboids with too large volumes.
Currently, I use a
StepSize = 10000 ... yes, I know it's not optimal (it doesn't find the result in its first iteration)but I deliberately keep it this way.
If
StepSize = 50 then fast() isn't faster than my original code.If
StepSize = 150000 then fast() isn't faster than my original code.That means for the original problem,
fast() is only truly faster if 50 < StepSize < 150000.
Note
Even though the code of fast() is shorter (and can be faster), I have a strange feeling about it:
somehow it needs a good guess but I haven't found a way to come up with a straightforward way to generate that guess.
I was stuck for a while because initially I stopped when I found a layer volume with at least 1000 matching cuboids (instead of exactly 1000).
There are a few volumes below the correct solution with more than 1000 cuboids.
Kristian Edlund visualized a nice way to enumerate the cubes added in each layer. His blog can found in my links.
Interactive test
You can submit your own input to my program and it will be instantly processed at my server:
This is equivalent toecho 10 | ./126
Output:
Note: the original problem's input 1000 cannot be entered
because just copying results is a soft skill reserved for idiots.
(this interactive test is still under development, computations will be aborted after one second)
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
#include <iostream> #include <vector> #include <set> #include <map> // a cuboid with 1+ added layers
struct Cuboid { // cuboid size const unsigned short width; const unsigned short height; const unsigned short depth; // wrapped several times const unsigned short layers; // compute volume with calculated() const unsigned int hullVolume; // create new cuboid Cuboid(unsigned short width_, unsigned short height_, unsigned short depth_, unsigned short layers_) : width(width_), height(height_), depth(depth_), layers(layers_), hullVolume(calculate()) {} // calculate volume of the most recent / outermost layer unsigned int calculate() const { // innermost hull auto result = 2 * ((unsigned int)width * height + (unsigned int)height * depth + (unsigned int)depth * width); // need just one layer ? if (layers == 1) return result; // add more layers auto increment = 4 * (width + height + depth); for (unsigned short current = 2; current <= layers; current++) { result += increment; increment += 8; } return result; } // for std::set bool operator<(const Cuboid& other) const { // volume if (hullVolume < other.hullVolume) return true; if (hullVolume > other.hullVolume) return false; // the following lines are arbitrary => they only need to be consistent // sides if (width < other.width) return true; if (width > other.width) return false; if (height < other.height) return true; if (height > other.height) return false; if (depth < other.depth) return true; if (depth > other.depth) return false; // layers return layers < other.layers; } }; // list of cuboids, sorted by volume of their outermost layer
std::set<Cuboid> todo; // count how many cuboid layers have a certain volume (looking for 1000)
std::map<unsigned int, unsigned int> count; // could be replaced by std::vector if you can estimate the upper limit // note: this information is implicitely stored in "todo" as well: count the consecutive cuboids with the same hullVolume
// add a cuboid with a certain amount of layers, return number of cuboids with the same hull volume
bool add(unsigned short width, unsigned short height, unsigned short depth, unsigned short layers) { // accept only width >= height >= depth if (width < height) return false; if (height < depth) return false; // create new cuboid Cuboid cuboid(width, height, depth, layers); // already queued ? if (todo.count(cuboid) != 0) return false; // add cuboid todo.insert(cuboid); count[cuboid.hullVolume]++; // successfully added return true; } const unsigned int Failed = 0; // find the correct result if you know an upper bound maxVolume, if not found return Failed
unsigned int fast(unsigned int stopIf, unsigned int maxVolume) { // allocate enough memory std::vector<unsigned int> count(maxVolume + 1, 0); // just four nested loops to generate all cuboids with hulls <= maxVolume // ensure that x >= y >= z to avoid enumerating some volume multiple times for (unsigned short x = 1; Cuboid(x,1,1,1).hullVolume <= maxVolume; x++) for (unsigned short y = 1; y <= x && Cuboid(x,y,1,1).hullVolume <= maxVolume; y++) for (unsigned short z = 1; z <= y && Cuboid(x,y,z,1).hullVolume <= maxVolume; z++) for (unsigned short layer = 1; ; layer++) { auto current = Cuboid(x,y,z,layer).hullVolume; if (current > maxVolume) break; count[current]++; } // find smallest hull volume that appears exactly 1000 times for (size_t i = 0; i < count.size(); i++) if (count[i] == stopIf) return i; // failed return Failed; } // forward declaration of my old helper code //unsigned int naive(unsigned int x, unsigned int y, unsigned int z, unsigned int layers);
int main() { // start old code to analyze a single cuboid //naive(3,2,1, 5); return 0; // look for that number of cuboids with the same volume unsigned int stopIf = 1000; std::cin >> stopIf; // ---------- fast enumeration ---------- // find solution if an upper limit of the result is known #define FAST_ENUMERATION #ifdef FAST_ENUMERATION const unsigned int StepSize = 10000; // I deliberately choose not the optimal value ! // assume that the result is below 10000, then 20000, ... until fast() returns > 0 for (unsigned int maxVolume = StepSize; ; maxVolume += StepSize) { auto current = fast(stopIf, maxVolume); // returns 0 if not found // found ? if (current != Failed) { std::cout << current << std::endl; return 0; } } #endif // ---------- slower enumeration ---------- // note: I found the correct result with this approach but later created the faster enumeration you find above // initial cuboid: one unit wide, high and deep with one layer around it add(1,1,1,1); unsigned int volume = 0; while (count[volume] != stopIf) { // pick cuboid with smallest volume and remove it auto current = *(todo.begin()); todo.erase(todo.begin()); volume = current.hullVolume; // enlarge cuboid add(current.width + 1, current.height, current.depth, current.layers); add(current.width, current.height + 1, current.depth, current.layers); add(current.width, current.height, current.depth + 1, current.layers); // add one layer add(current.width, current.height, current.depth, current.layers + 1); } // display result std::cout << volume << std::endl; return 0; } // ---------- compute hull volume, slow approach ----------
// a single cube that is part of an cuboid (more or less a coordinate)
struct Cube { // coordinates const int x, y, z; // create new cube Cube(int xx, int yy, int zz) : x(xx), y(yy), z(zz) {} // for std::set bool operator<(const Cube& other) const { if (x < other.x) return true; if (x > other.x) return false; if (y < other.y) return true; if (y > other.y) return false; return z < other.z; } }; unsigned int naive(unsigned int x, unsigned int y, unsigned int z, unsigned int layers) { // keep track of all cubes belonging to the shape std::set<Cube> cuboid; // cubes added in the most recent layer std::vector<Cube> hull; // initial shape for (int xx = 0; xx < (int)x; xx++) for (int yy = 0; yy < (int)y; yy++) for (int zz = 0; zz < (int)z; zz++) { Cube current(xx, yy, zz); cuboid.insert(current); hull.push_back(current); } // add desired numbers of layers for (unsigned int layer = 1; layer <= layers; layer++) { std::vector<Cube> next; for (auto current : hull) { // grow in each direction x,y,z Cube left (current.x - 1, current.y, current.z); Cube right(current.x + 1, current.y, current.z); Cube down (current.x, current.y - 1, current.z); Cube up (current.x, current.y + 1, current.z); Cube back (current.x, current.y, current.z - 1); Cube front(current.x, current.y, current.z + 1); // add cube (if not already existing) if (cuboid.count(left) == 0) { cuboid.insert(left); next.push_back(left); } if (cuboid.count(right) == 0) { cuboid.insert(right); next.push_back(right); } if (cuboid.count(down) == 0) { cuboid.insert(down); next.push_back(down); } if (cuboid.count(up) == 0) { cuboid.insert(up); next.push_back(up); } if (cuboid.count(back) == 0) { cuboid.insert(back); next.push_back(back); } if (cuboid.count(front) == 0) { cuboid.insert(front); next.push_back(front); } } std::cout << "layer " << layer << ": " << "C(" << x << "," << y << "," << z << ")=" << next.size(); if (layer > 1) std::cout << " delta=" << next.size() - hull.size(); std::cout << std::endl; // next iteration hull = std::move(next); } return hull.size(); }
This solution contains 40 empty lines, 57 comments and 7 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in 0.04 seconds on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
August 18, 2017 submitted solution
August 18, 2017 added comments
Difficulty
Project Euler ranks this problem at 55% (out of 100%).
Links
projecteuler.net/thread=126 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
C# www.mathblog.dk/project-euler-126-cubes-cover-cuboid/ (written by Kristian Edlund)
C# github.com/HaochenLiu/My-Project-Euler/blob/master/126.cs (written by Haochen Liu)
Python github.com/Meng-Gen/ProjectEuler/blob/master/126.py (written by Meng-Gen Tsai)
C++ github.com/roosephu/project-euler/blob/master/126.cpp (written by Yuping Luo)
C++ github.com/steve98654/ProjectEuler/blob/master/126.cpp
C github.com/zmwangx/Project-Euler/blob/master/126/126.c (written by Zhiming Wang)
Java github.com/thrap/project-euler/blob/master/src/Java/Problem126.java (written by Magnus Solheim Thrap)
Go github.com/frrad/project-euler/blob/master/golang/Problem126.go (written by Frederick Robinson)
Mathematica github.com/steve98654/ProjectEuler/blob/master/126.nb
Haskell github.com/frrad/project-euler/blob/master/haskell/Problem126.hs (written by Frederick Robinson)
Perl github.com/shlomif/project-euler/blob/master/project-euler/126/euler-126.pl (written by Shlomi Fish)
Rust github.com/gifnksm/ProjectEulerRust/blob/master/src/bin/p126.rs
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 | 807 | 808 | 809 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 125 - Palindromic sums |

|
abc-hits - problem 127 >> |