| << problem 504 - Square on the Inside |

|
5-smooth totients - problem 516 >> |
Problem 510: Tangent Circles
(see projecteuler.net/problem=510)
Circles A and B are tangent to each other and to line L at three distinct points.
Circle C is inside the space between A, B and L, and tangent to all three.
Let r_A, r_B and r_C be the radii of A, B and C respectively.
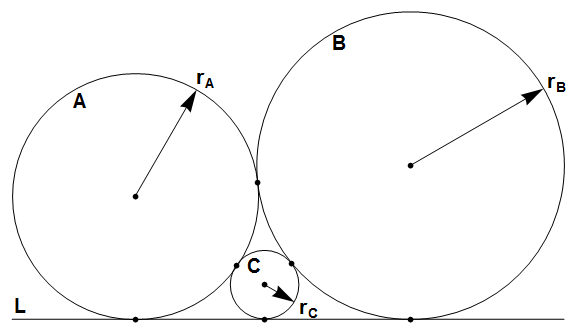
Let S(n) = sum{r_A + r_B + r_C}, for 0 < r_A <= r_B <= n where r_A, r_B and r_C are integers.
The only solution for 0 < r_A <= r_B <= 5 is r_A = 4, r_B = 4 and r_C = 1, so S(5) = 4 + 4 + 1 = 9.
You are also given S(100) = 3072.
Find S(10^9).
My Algorithm
A simple bruteForce() function easily verifies S(100) (and even manages to solve S(1000))
but then falls apart due to rounding problems and - more import - performance issues.
However, it reveals a few things:
- most solutions are multiples of (4,4,1)
- and in general: for each solution all of its multiples are solutions, too
- if I remove these multiples, then the basic solutions are squares only
(which is not really solved yet: I still have some severe performance issues but they aren't related to the geometric solution).
Anyway, I learnt that these kind of problems have been around for ages and were analyzed by Appolonius more than 2000 years ago (see en.wikipedia.org/wiki/Problem_of_Apollonius).
Renè Descartes found a great equation (see en.wikipedia.org/wiki/Descartes'_theorem) if four circles touch each other and their curvature is k = 1 / r
(1) (k_1 + k_2 + k_3 + k_4)^2 = 2 (k_1^2 + k_2^2 + k_3^2 + k_4^2)
Unfortunately, I don't have four but three circles and a line ...
and fortunately, if I set k = 0 then the formula solves the case of three circles and a line, too !
Now the whole equation simplifies to
(2) (k_A + k_B + k_C)^2 = 2 (k_A^2 + k_B^2 + k_C^2)
If I solve for k_C then
(3) sqrt{k_C} = sqrt{k_A} + sqrt{k_B}
And with regards to the radii instead of the curvatures (remember: k = 1 / r)
(4) dfrac{1}{sqrt{r_C}} = dfrac{1}{sqrt{r_A}} + dfrac{1}{sqrt{r_B}}
As I said before, all solutions are squares (or multiples of squares).
If I assume a = sqrt{r_A} and b = sqrt{r_B} and c = sqrt{r_C} then:
(5) dfrac{1}{c} = dfrac{1}{a} + dfrac{1}{b}
Solved for c
(6) c = dfrac{ab}{a+b}
My program iterates over all a and b where b < a (that's different from the problem statement but it doesn't affect the result).
If a^2 b^2 is a multiple of a^2 + b^2 then I have found another c^2.
That means I have found a triple (a^2, b^2, c^2) = (r_A, r_B, r_C).
It's possible that the multiples of squares are squares, too.
Therefore I have to make sure that they are coprime (gcd(a,b,c) = 1) otherwise they would be counted twice.
The sum of all multiples of r_A + r_B + r_C is based on the triangular numbers (see
triangle()).If m is the number of multiples of a basic solution:
(7) m = dfrac{limit}{r_A} → because I defined r_A >= r_B
(8) sum_{k=1..m}{k} = dfrac{m(m+1)}{2}
(9) sum_{k=1..m}{k (r_A + r_B + r_C)} = (r_A + r_B + r_C) dfrac{m(m+1)}{2}
Alternative Approaches
After submitting my solution I saw in the Project Euler forum that you can heavily re-arrange the for-loops such that the solution is found in a few milliseconds.
Interactive test
You can submit your own input to my program and it will be instantly processed at my server:
This is equivalent toecho 100 | ./510
Output:
Note: the original problem's input 1000000000 cannot be entered
because just copying results is a soft skill reserved for idiots.
(this interactive test is still under development, computations will be aborted after one second)
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
#include <iostream> #include <cmath> // ---------- taken from my toolbox ----------
// greatest common divisor
template <typename T> T gcd(T a, T b) { while (a != 0) { T c = a; a = b % a; b = c; } return b; } // ---------- brute force solution (not used anymore) ----------
// try all combinations of a,b,c
unsigned int bruteForce(unsigned int limit) { // accept solution if left side of the equation of Descartes theorem // doesn't differ by more than epsilon from the right side const double Epsilon = 0.0000000000001; // sum of all valid a,b,c unsigned int result = 0; for (unsigned int a = 1; a <= limit; a++) for (unsigned int b = 1; b <= a; b++) for (unsigned int c = 1; c <= b; c++) { // curvatures double k1 = 1.0 / a; double k2 = 1.0 / b; double k3 = 1.0 / c; // both sides of the equation double leftSide = (k1 + k2 + k3) * (k1 + k2 + k3); double rightSide = 2 * (k1*k1 + k2*k2 + k3*k3); // acceptable error ? if (fabs(leftSide - rightSide) < Epsilon) { auto sum = a + b + c; //std::cout << a << "+" << b << "+" << c << "=" << sum << std::endl; result += sum; } } return result; } // ---------- relevant code ----------
// compute triangular number
unsigned long long triangle(unsigned int n) { // sum of 1+2+3+...+n // see https://en.wikipedia.org/wiki/Triangular_number unsigned long long nn = n; return nn * (nn + 1) / 2; } typedef long long Number; unsigned long long evaluate(unsigned int limit) { // all multiples of the basic 4+4+1 solution unsigned long long result = 0; // all multiples of a^2, b^2, c^2 // where 1/c2 = (1/a2 + 1/b2) + 2sqrt(1/a2 * 1/b2) // => sqrt(1/c2) = sqrt(1/a2) + sqrt(1/b2) // => 1/c = 1/a + 1/b // => c = a*b / (a+b) for (unsigned long long a = 1; a*a < limit; a++) for (unsigned long long b = 1; b <= a; b++) { // numerator = a*a * b*b auto a2 = a*a; auto b2 = b*b; auto numerator = a2 * b2; // denominator = (a+b)^2 auto denominator = (a+b) * (a+b); // c^2 must be an integer auto c2 = numerator / denominator; // no remainder left by the previous divison ? if (c2 * denominator != numerator) continue; // all values must be coprime if (gcd(gcd(a2, b2), c2) == 1) { auto multiples = limit / (unsigned int)a2; auto sum = (a2 + b2 + c2) * triangle(multiples); result += sum; } } return result; } int main() { unsigned int limit = 1000000000; std::cin >> limit; //std::cout << bruteForce(limit) << std::endl; std::cout << evaluate (limit) << std::endl; return 0; }
This solution contains 16 empty lines, 27 comments and 2 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in 4.2 seconds on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
September 8, 2017 submitted solution
September 8, 2017 added comments
Difficulty
Project Euler ranks this problem at 30% (out of 100%).
Links
projecteuler.net/thread=510 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
Python github.com/Meng-Gen/ProjectEuler/blob/master/510.py (written by Meng-Gen Tsai)
Python github.com/roosephu/project-euler/blob/master/510.py (written by Yuping Luo)
C++ github.com/roosephu/project-euler/blob/master/510.cpp (written by Yuping Luo)
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 | 807 | 808 | 809 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 504 - Square on the Inside |

|
5-smooth totients - problem 516 >> |