| << problem 571 - Super Pandigital Numbers |

|
47-smooth triangular numbers - problem 581 >> |
Problem 577: Counting hexagons
(see projecteuler.net/problem=577)
An equilateral triangle with integer side length n >= 3 is divided into n^2 equilateral triangles with side length 1 as shown in the diagram below.
The vertices of these triangles constitute a triangular lattice with dfrac{(n+1)(n+2)}{2} lattice points.
Let H(n) be the number of all regular hexagons that can be found by connecting 6 of these points.
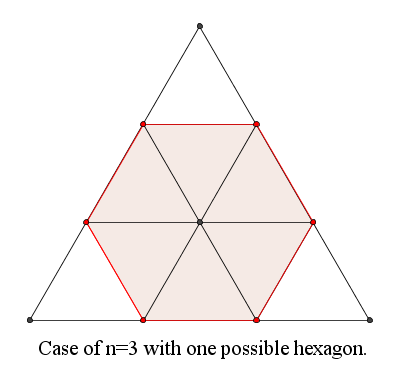
For example, H(3)=1, H(6)=12 and H(20)=966.
Find sum_{n=3}^12345{H(n)}.
My Algorithm
My initial brute-force algorithm works as follows:
- assume that every hexagon's center is a lattice point, too (bold assumption - but seems to works for all H(n))
- for each such lattice point, compute the distances to every other lattice point
- compute the angle as well
- keep a data structure of all distances and angles for each lattice point
- round values to avoid errors due to numeric imprecision
- six points with the same distance
- their angles are 60 degrees apart from each other
bruteForce() function computes H(20) = 966 in a few milliseconds. For n > 100 it becomes pretty slow, though.I entered the values H(3), H(4), H(5), etc. (1,3,6,12,21,33,51,75,105,145,195,255,...) in www.oeis.org and found the sequence OEIS A011779.
Unfortunately I couldn't handle the series expansion in a few lines of C++ code.
Since the "larger" hexagons appear when n mod 3 == 0 I split the sequence into three parts:
- H(3), H(6), H( 9), etc. (1,12,51,145,...) → OEIS A236770:
- H(4), H(7), H(10), etc. (3,21,75,195,...) → OEIS A228317:
- H(5), H(8), H(11), etc. (6,33,105,255,...)
However, I noticed that every H(n) for n mod 3 == 2 is a multiple of 3. And voila: 2,11,35,85 is OEIS A000914.
In the end I have a simple loop from 3 to 12345 that calls
A236770(), A228317() or A000914(), depending on n % 3.
Note
Honestly, I thought that my bruteForce() results might be wrong even for small n because of numeric imprecisions.
But the code proved to be quite stable: all H(n) for n <= 100 are correct (I didn't verify larger n).
Today is the end of the year - and the end of the fiscal year, too, so I donated 10 bucks to OEIS. For tax reasons :-)
Interactive test
You can submit your own input to my program and it will be instantly processed at my server:
This is equivalent toecho 20 | ./577
Output:
Note: the original problem's input 12345 cannot be entered
because just copying results is a soft skill reserved for idiots.
(this interactive test is still under development, computations will be aborted after one second)
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
#include <iostream> #include <vector> #include <map> #include <algorithm> #include <cmath> // ---------- brute force up to n=100 ----------
const auto PI = 3.14159265358979323846264; const auto Precision = 0.00001; // 2D point
struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) { } // distance between two points double distance(const Point& other) const { auto dx = other.x - x; auto dy = other.y - y; return sqrt(dx*dx + dy * dy); // I could skip sqrt because the squared distance works as well } // angle (in degrees, always positive) double angle(const Point& other) const { auto dx = other.x - x; auto dy = other.y - y; auto radian = atan2(dy, dx); // convert to degrees auto degrees = radian * 180 / PI; if (degrees < 0) degrees += 360; return degrees; } }; // round a double with a certain precision, e.g. round(5.126, 0.01) = 5.13
double round(double a, double precision) { return round(a / precision) * precision; } // look for hexagons using polar coordinates
unsigned long long bruteForce(unsigned int size) { // horizontal and vertical distance between two neighbors in the lattice / grid double dx = 1; double dy = sqrt(3.0) / 2; // height of https://en.wikipedia.org/wiki/Equilateral_triangle // generate all points std::vector<Point> points; auto numPoints = (size + 1) * (size + 2) / 2; for (unsigned int gridY = 0; gridY <= size; gridY++) { // position of the left-most point in each row double y = gridY * dy; double x = gridY * dx / 2; // all points in the current row auto width = size - gridY; for (unsigned int gridX = 0; gridX <= width; gridX++) { points.push_back(Point(x, y)); x += dx; } } // for each points: compute polar coordinates of the vector to each other point std::vector<std::map<double, std::vector<double>>> polar; // map: distance => angles for (auto i : points) { // add one element polar.resize(polar.size() + 1); // direct access to it auto& current = polar.back(); for (auto j : points) { auto distance = i.distance(j); auto angle = i.angle(j); // avoid precision issues distance = round(distance, Precision); angle = round(angle, Precision); if (distance > 0) current[distance].push_back(angle); } } // find hexagons amidst these polar coordinates: // six points having the same distance where angles are (2*pi) / 6 apart unsigned long long numFound = 0; for (unsigned int point = 0; point < numPoints; point++) { for (auto& distance : polar[point]) { auto& candidates = distance.second; // hexagon impossible ? if (candidates.size() < 6) continue; // look for subsets with 6 elements { start, start+60, start+120, // start+180, start+240, start+300 } std::sort(candidates.begin(), candidates.end()); for (auto start : candidates) { // smallest angle must be 0 <= start < 60 (in degrees) if (start >= 60) // hexagon has 6 sides, so 360 / 6 = 60 break; // check if angle+60, +120, +180, ... exist bool valid = true; for (auto next = start + 60; next < 360; next += 60) // note: need the same rounding as used before ! if (!std::binary_search(candidates.begin(), candidates.end(), round(next, Precision))) { valid = false; break; } // yes, found another hexagon if (valid) numFound++; } } } return numFound; } // ---------- super-fast algorithm ----------
// sequence oeis.org/A000914
unsigned long long A000914(unsigned long long n) { return n * (n+1) * (n+2) * (3*n+5) / 24; } // sequence oeis.org/A228317
unsigned long long A228317(unsigned long long n) { return n * (n-1) * (n-2) * (3*n-5) / 8; } // sequence oeis.org/A236770
unsigned long long A236770(unsigned long long n) { return n * (n+1) * (3*n*n + 3*n - 2) / 8; } int main() { unsigned int size = 12345; // n std::cin >> size; // brute force //std::cout << bruteForce(size) << std::endl; // indices for A000914, A228317 and A236770 unsigned int i000914 = 1; unsigned int i228317 = 3; unsigned int i236770 = 1; unsigned long long sum = 0; // no hexagons below n = 3 for (unsigned int n = 3; n <= size; n++) { unsigned long long fast = 0; // method of calculation depends on n mod 3 switch (n % 3) { case 0: fast = A236770(i236770++); break; case 1: fast = A228317(i228317++); break; case 2: fast = 3 * A000914(i000914++); break; } sum += fast; } // that's it ! std::cout << sum << std::endl; return 0; }
This solution contains 28 empty lines, 34 comments and 5 preprocessor commands.
Changelog
December 31, 2017 submitted solution
December 31, 2017 added comments
Difficulty
Project Euler ranks this problem at 20% (out of 100%).
Links
projecteuler.net/thread=577 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
Python github.com/evilmucedin/project-euler/blob/master/euler577/euler577.py (written by Den Raskovalov)
Python github.com/roosephu/project-euler/blob/master/577.py (written by Yuping Luo)
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 | 807 | 808 | 809 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 571 - Super Pandigital Numbers |

|
47-smooth triangular numbers - problem 581 >> |