| << problem 149 - Searching for a maximum-sum subsequence |

|
Paper sheets of standard sizes: an expected ... - problem 151 >> |
Problem 150: Searching a triangular array for a sub-triangle having minimum-sum
(see projecteuler.net/problem=150)
In a triangular array of positive and negative integers, we wish to find a sub-triangle such that the sum of the numbers it contains is the smallest possible.
In the example below, it can be easily verified that the marked triangle satisfies this condition having a sum of −42.
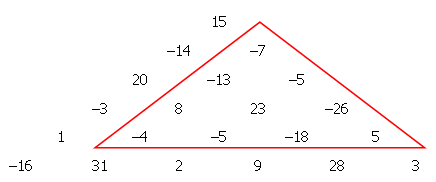
We wish to make such a triangular array with one thousand rows, so we generate 500500 pseudo-random numbers s_k in the range \pm 2^19,
using a type of random number generator (known as a Linear Congruential Generator) as follows:
t := 0
for k = 1 up to k = 500500:
t := (615949*t + 797807) modulo 220
s_k := t-219
Thus: s_1 = 273519, s_2 = -153582, s_3 = 450905 etc
Our triangular array is then formed using the pseudo-random numbers thus:
s_1
s_2 s_3
s_4 s_5 s_6
s_7 s_8 s_9 s_10
...
Sub-triangles can start at any element of the array and extend down as far as we like
(taking-in the two elements directly below it from the next row, the three elements directly below from the row after that, and so on).
The "sum of a sub-triangle" is defined as the sum of all the elements it contains.
Find the smallest possible sub-triangle sum.
My Algorithm
My solution can be called a "tweaked brute-force approach".
I store the triangle in a 2D array, where the number of "columns" of each row varies: only one at the top and columns = rows at the bottom.
For each cell (x,y) I walk through all possible triangles (x, y),(x + increment, y),(x, y + increment).
For increment = 0, the sum is just the value found in triangle[x][y].
For increment = 1, I add all the two values of the next row to the result of increment = 0, thus triangle[x][y] + triangle[x][y+1] + triangle[x+1][y+1]
In general: for each increment > 0, I add all the two values of the next row to the result of increment - 1.
Whenever my sum is lower than the previously lowest sum, I store it (Hackerrank: store every sum).
Repeatedly adding numbers in the same row turned out to be a performance bottleneck.
In step 2 of my code, a second container called sums is created which contains sums[x][y] = sum(triangle[0..x][y]) (similar to a running total).
Then sum(triangle[x1..x2][y]) = sums[x2][y] - sums[x1 - 1][y] (except when x1 is zero).
In the end, this optimization reduced runtime from 20 seconds to just 0.4 seconds.
Modifications by HackerRank
Hackerrank provides all input data (instead of the Linear Congruential Generator) and asks you to print
the n smallest sub-triangle sums.
Because of the large number of sums (= high memory usage), I repeatedly sort all values of results and erase all but the smallest n.
I am fully aware that the high number if #ifdef severely decreases readability of my code.
Interactive test
You can submit your own input to my program and it will be instantly processed at my server:
This is equivalent toecho 10 | ./150
Output:
Note: the original problem's input 1000 cannot be entered
because just copying results is a soft skill reserved for idiots.
(this interactive test is still under development, computations will be aborted after one second)
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
The code contains #ifdefs to switch between the original problem and the Hackerrank version.
Enable #ifdef ORIGINAL to produce the result for the original problem (default setting for most problems).
#include <iostream> #include <vector> #include <algorithm> // pseudo-random number generator
int lcg() { static long long seed = 0; seed = (615949 * seed + 797807) % (1 << 20); return int(seed - (1 << 19)); } int main() { // indexed: triangle[y][x] where y denotes the row std::vector<std::vector<int>> triangle; // step 1: initialize the triangle (either with random data or from STDIN) #define ORIGINAL #ifdef ORIGINAL // 1000 rows unsigned int maxSize = 1000; std::cin >> maxSize; // fill with (pseudo) random data triangle.resize(maxSize); for (size_t y = 0; y < triangle.size(); y++) for (size_t x = 0; x <= y; x++) triangle[y].push_back(lcg()); #else size_t size; size_t maxResults; std::cin >> size >> maxResults; triangle.resize(size); for (size_t y = 0; y < size; y++) for (size_t x = 0; x <= y; x++) { int current; std::cin >> current; triangle[y].push_back(current); } #endif // step 2: build another triangle called "sums" where each cell is sum(triangle[y][0..x]) std::vector<std::vector<int>> sums(triangle.size()); for (size_t y = 0; y < triangle.size(); y++) { // same size sums[y].resize(triangle[y].size()); // store running sum of all cells to the left of the current cell, including the current, too int rowSum = 0; for (size_t x = 0; x <= y; x++) { rowSum += triangle[y][x]; sums[y][x] = rowSum; } } // store the smallest sums #ifdef ORIGINAL auto result = triangle[0][0]; // simplify if only one sum #else std::vector<int> results; // needs sorting, pruning, etc. #endif // analyze all positions for (size_t y = 0; y < triangle.size(); y++) { for (size_t x = 0; x <= y; x++) { // smallest triangle consists of a single-cell auto sum = triangle[y][x]; // better than before ? #ifdef ORIGINAL if (result > sum) result = sum; #else results.push_back(sum); #endif // add rows auto maxSize = triangle.size() - y; for (size_t current = 1; current < maxSize; current++) { // compute sum(triangle[y + rows][x ... x + rows]) // add singles values, "old way" //for (size_t scan = x; scan <= x + current; scan++) // sum += triangle[y + current][scan]; // access pre-computed running sums from step 2, "new way" auto rowSum = sums[y + current][x + current]; if (x > 0) rowSum -= sums[y + current][x - 1]; sum += rowSum; // better than before ? #ifdef ORIGINAL if (result > sum) result = sum; #else results.push_back(sum); #endif } } #ifndef ORIGINAL // prune sums std::sort(results.begin(), results.end()); if (results.size() > maxResults) results.erase(results.begin() + maxResults, results.end()); #endif } // show result #ifdef ORIGINAL std::cout << result << std::endl; #else for (auto x : results) std::cout << x << std::endl; #endif return 0; }
This solution contains 17 empty lines, 21 comments and 21 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in 0.4 seconds on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
Peak memory usage was about 7 MByte.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
July 5, 2017 submitted solution
July 5, 2017 added comments
Hackerrank
see https://www.hackerrank.com/contests/projecteuler/challenges/euler150
My code solves 10 out of 10 test cases (score: 100%)
Difficulty
Project Euler ranks this problem at 55% (out of 100%).
Hackerrank describes this problem as easy.
Note:
Hackerrank has strict execution time limits (typically 2 seconds for C++ code) and often a much wider input range than the original problem.
In my opinion, Hackerrank's modified problems are usually a lot harder to solve. As a rule thumb: brute-force is rarely an option.
Links
projecteuler.net/thread=150 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
Python github.com/Meng-Gen/ProjectEuler/blob/master/150.py (written by Meng-Gen Tsai)
Python github.com/nayuki/Project-Euler-solutions/blob/master/python/p150.py (written by Nayuki)
C++ github.com/roosephu/project-euler/blob/master/150.cpp (written by Yuping Luo)
C++ github.com/smacke/project-euler/blob/master/cpp/150.cpp (written by Stephen Macke)
Java github.com/HaochenLiu/My-Project-Euler/blob/master/150.java (written by Haochen Liu)
Java github.com/nayuki/Project-Euler-solutions/blob/master/java/p150.java (written by Nayuki)
Java github.com/thrap/project-euler/blob/master/src/Java/Problem150.java (written by Magnus Solheim Thrap)
Go github.com/frrad/project-euler/blob/master/golang/Problem150.go (written by Frederick Robinson)
Mathematica github.com/steve98654/ProjectEuler/blob/master/150.nb
Perl github.com/shlomif/project-euler/blob/master/project-euler/150/euler-150.pl (written by Shlomi Fish)
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 | 807 | 808 | 809 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 149 - Searching for a maximum-sum subsequence |

|
Paper sheets of standard sizes: an expected ... - problem 151 >> |