| << problem 197 - Investigating the behaviour of a recursively ... |

|
Find the 200th prime-proof sqube containing ... - problem 200 >> |
Problem 199: Iterative Circle Packing
(see projecteuler.net/problem=199)
Three circles of equal radius are placed inside a larger circle such that each pair of circles is tangent to one another and the inner circles do not overlap.
There are four uncovered "gaps" which are to be filled iteratively with more tangent circles.
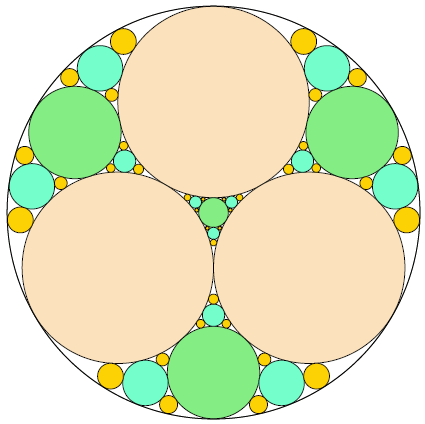
At each iteration, a maximally sized circle is placed in each gap, which creates more gaps for the next iteration.
After 3 iterations (pictured), there are 108 gaps and the fraction of the area which is not covered by circles is 0.06790342, rounded to eight decimal places.
What fraction of the area is not covered by circles after 10 iterations?
Give your answer rounded to eight decimal places using the format x.xxxxxxxx .
My Algorithm
Two days ago I published my solution to problem 510 where I mentioned that I got the final insights to solve 510 and 199 by going to a museum:
by pure chance I saw some ancient drawings that looked pretty much like the circles in the example.
And they had a name: Apollonian gasket (see en.wikipedia.org/wiki/Apollonian_gasket)
The Wikipedia page linked to the Descartes' theorem (see en.wikipedia.org/wiki/Descartes'_theorem) which comes with a nice formula:
(1) (k_1 + k_2 + k_3 + k_4)^2 = 2(k_1^2 + k_2^2 +k_3^2 +k_4^2)
So when there are four circles touching each other the their "curvatures" k always fulfil that equation.
The curvate is defined to be k = 1/r and, even more interesting, it can be negative when a circle touches the other with its inside.
That's only the case for the outermost circle.
If three curvatures are known then (1) can be transformed to compute the fourth:
(2) k_4 = k_1 + k_2 + k_3 \pm 2 sqrt{k_1 k_2 + k_2 k_3 + k_1 k_3}
I started with the three circles at level 1 and defined their radius to be 1. I found two circles: one between the three and one outside the three.
The outermost circle (level 0) must be the one with the larger radius which turned out to be 3 - 2 sqrt{3} approx 2.1547.
Since it contains all other circle its curvature must be negative: k = - dfrac{1}{3 - 2 sqrt{3}}
My function evaluate() recursively determines the the sum of the area covered by the "children" of three circles
with curvatures k1, k2 and k3 up to recursion level depth.
There are two distinct groups of "parents":
- three V-shaped areas enclosed by the outermost circle and two circles at level 1
- the small area between the three circles at level 1
Now I know the area of all children (up to level 10). I haven't added the area of the three circles at level 1 yet.
Their sum divided by the area of the outermost circle gives the percentage of coverage, and 100% minus this value is the final result.
Note
evalute() will often be called with the same parameter set and becomes pretty slow beyond level 16.
I tried to add a small memoization scheme (same trick as always ...) but ended up slowing the the program for the default input 10 considerably.
Therefore I removed it - even though it's more efficient for higher input values.
Interactive test
You can submit your own input to my program and it will be instantly processed at my server:
This is equivalent toecho 3 | ./199
Output:
Note: the original problem's input 10 cannot be entered
because just copying results is a soft skill reserved for idiots.
(this interactive test is still under development, computations will be aborted after one second)
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
#include <iostream> #include <cmath> // return area of a circle
double getArea(double radius) { return radius * radius * 3.14159265358979323846 / 4; } // return sum of touching circles' areas including their children
double evaluate(double k1, double k2, double k3, unsigned int depth) { // https://en.wikipedia.org/wiki/Descartes%27_theorem auto k4 = k1 + k2 + k3 + 2 * sqrt(k1*k2 + k2*k3 + k1*k3); // area of the current circle auto radius = 1 / k4; auto area = getArea(radius); // done ? if (depth == 1) return area; // keep going ... return area + evaluate(k1, k2, k4, depth - 1) + evaluate(k2, k3, k4, depth - 1) + evaluate(k1, k3, k4, depth - 1); } int main() { // nesting level unsigned int depth = 10; std::cin >> depth; // the big circle can be computed with Descartes theorem // k1 = k2 = k3 = 1 and k4 = k1 + k2 + k3 + 2*sqrt(k1 + k2 + k3) // => k4 = 3 +- 2*sqrt(3) // case A: k4 = 3 + 2*sqrt(3) => radius approx. 0.1547 => that's the small circle between the three circles // case B: k4 = 3 - 2*sqrt(3) => radius approx. 2.1547 => that's the big circle I'm looking for auto outerK = 3 - 2 * sqrt(3); auto outerRadius = -1 / outerK; // note: outerK is negative // the first three circle have radius = 1 auto innerRadius = 1.0; auto innerK = 1 / innerRadius; // (fully covered) area of the first three circles auto initial = 3 * getArea(innerRadius); // (partially full) three identical V-shaped areas between two circles and the big circle auto vShaped = evaluate(outerK, innerK, innerK, depth); // (partially full) small area between the first three circles auto middle = evaluate(innerK, innerK, innerK, depth); // total covered area auto result = initial + 3 * vShaped + middle; // as a percentage of the big circle result /= getArea(outerRadius); // empty = 100% - covered std::cout << 1 - result << std::endl; return 0; }
This solution contains 9 empty lines, 19 comments and 2 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in less than 0.01 seconds on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
September 10, 2017 submitted solution
September 10, 2017 added comments
Difficulty
Project Euler ranks this problem at 70% (out of 100%).
Links
projecteuler.net/thread=199 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
Python github.com/Meng-Gen/ProjectEuler/blob/master/199.py (written by Meng-Gen Tsai)
C++ github.com/roosephu/project-euler/blob/master/199.cpp (written by Yuping Luo)
Java github.com/HaochenLiu/My-Project-Euler/blob/master/199.java (written by Haochen Liu)
Java github.com/thrap/project-euler/blob/master/src/Java/Problem199.java (written by Magnus Solheim Thrap)
Mathematica github.com/LaurentMazare/ProjectEuler/blob/master/e199.ml (written by Laurent Mazare)
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 | 807 | 808 | 809 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 197 - Investigating the behaviour of a recursively ... |

|
Find the 200th prime-proof sqube containing ... - problem 200 >> |