| << problem 89 - Roman numerals |

|
Right triangles with integer coordinates - problem 91 >> |
Problem 90: Cube digit pairs
(see projecteuler.net/problem=90)
Each of the six faces on a cube has a different digit (0 to 9) written on it; the same is done to a second cube.
By placing the two cubes side-by-side in different positions we can form a variety of 2-digit numbers.
For example, the square number 64 could be formed:
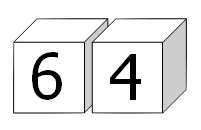
In fact, by carefully choosing the digits on both cubes it is possible to display all of the square numbers below one-hundred:
01, 04, 09, 16, 25, 36, 49, 64, and 81.
For example, one way this can be achieved is by placing {0, 5, 6, 7, 8, 9} on one cube and {1, 2, 3, 4, 8, 9} on the other cube.
However, for this problem we shall allow the 6 or 9 to be turned upside-down so that an arrangement like {0, 5, 6, 7, 8, 9} and {1, 2, 3, 4, 6, 7}
allows for all nine square numbers to be displayed; otherwise it would be impossible to obtain 09.
In determining a distinct arrangement we are interested in the digits on each cube, not the order.
{1, 2, 3, 4, 5, 6} is equivalent to {3, 6, 4, 1, 2, 5}
{1, 2, 3, 4, 5, 6} is distinct from {1, 2, 3, 4, 5, 9}
But because we are allowing 6 and 9 to be reversed, the two distinct sets in the last example both represent the extended set {1, 2, 3, 4, 5, 6, 9}
for the purpose of forming 2-digit numbers.
How many distinct arrangements of the two cubes allow for all of the square numbers to be displayed?
My Algorithm
[TODO] write down a few words
Interactive test
You can submit your own input to my program and it will be instantly processed at my server:
This is equivalent toecho "3 1" | ./90
Output:
Note: the original problem's input 9 2 cannot be entered
because just copying results is a soft skill reserved for idiots.
(this interactive test is still under development, computations will be aborted after one second)
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
#include <algorithm> #include <vector> #include <iostream> // all sides of a dice
typedef std::vector<unsigned int> Dice; // each cube has 6 different sides, we can choose any 6 out of 10
const Dice Sides = { 0,1,2,3,4,5,6,7,8,9 }; const unsigned int Skip = 0; const unsigned int Take = 1; // if container[x] is Take, then Sides[x] is part of the dice
const std::vector<unsigned int> Initial = { Skip,Skip,Skip,Skip, Take,Take,Take,Take,Take,Take }; const std::vector<unsigned int> Unused = { Take }; int main() { unsigned int dices = 2; unsigned int limit = 9; // up to the 9th square (9^2 = 81) std::cin >> limit >> dices; // Hackerrank extended the problem to three dices const unsigned int AllDices = 3; unsigned int maxSquare = 0; // generate all square numbers std::vector<unsigned short> squares; for (unsigned int i = 1; i <= limit; i++) { auto reduce = i*i; maxSquare = reduce; std::vector<unsigned int> digits; // no matter what, always generate a three-digit square (maybe with some leading zeros) for (unsigned int j = 0; j < AllDices; j++) { auto digit = reduce % 10; reduce /= 10; // convert all 9s to 6s if (digit == 9) digit = 6; digits.push_back(digit); } // digits in ascending order std::sort(digits.begin(), digits.end()); // convert to a fingerprint // e.g. 9^2 = 081 (with leading zero) // => 018 (sorted) // => 18 (sorted, converted to an integer) auto sortedSquare = digits[0] * 100 + digits[1] * 10 + digits[2]; if (std::find(squares.begin(), squares.end(), sortedSquare) == squares.end()) squares.push_back(sortedSquare); } // will contain all solutions unsigned int valid = 0; // all possible label combinations for first dice Dice dice1, dice2, dice3; auto open = squares; auto permutationDice1 = Initial; auto permutationDice2 = Initial; auto permutationDice3 = Initial; do { dice1.clear(); for (size_t i = 0; i < permutationDice1.size(); i++) if (permutationDice1[i] == Take) dice1.push_back(Sides[i]); // if both 6 and 9 are contained, then they behave identical //if (permutationDice1[6] == Take && permutationDice1[9] == Take) //dice1.pop_back(); // second dice is "lexicographically" bigger than or equal to first dice permutationDice2 = (dices >= 2 ? permutationDice1 : Unused); do { dice2.clear(); for (size_t i = 0; i < permutationDice2.size(); i++) if (permutationDice2[i] == Take) dice2.push_back(Sides[i]); // some digits need to occur at least twice if (maxSquare >= 100) { // 100 requires two zeros, so we must already have at least one if (std::count(dice1.begin(), dice1.end(), 0) + std::count(dice2.begin(), dice2.end(), 0) < 1) continue; } if (maxSquare >= 144) { // 144 requires two 4s, so we must have at least one by now if (std::count(dice1.begin(), dice1.end(), 4) + std::count(dice2.begin(), dice2.end(), 4) < 1) continue; } // if less than three dices are requested then add a dummy dice with one side permutationDice3 = (dices == 3 ? permutationDice2 : Unused); do { dice3.clear(); for (size_t i = 0; i < permutationDice3.size(); i++) if (permutationDice3[i] == Take) dice3.push_back(Sides[i]); // simple pre-check unsigned int frequency[10] = { 0,0,0,0,0, 0,0,0,0,0 }; for (auto x : dice1) frequency[x]++; for (auto x : dice2) frequency[x]++; for (auto x : dice3) frequency[x]++; // for performance optimization only: reject impossible combinations if (frequency[1] < 1) continue; if (maxSquare >= 4 && frequency[4] < 1) continue; if (maxSquare >= 25 && frequency[2] < 1) continue; if (maxSquare >= 25 && frequency[5] < 1) continue; if (maxSquare >= 36 && frequency[3] < 1) continue; if (maxSquare >= 81 && frequency[8] < 1) continue; if (maxSquare >= 100 && frequency[0] < 2) continue; if (maxSquare >= 144 && frequency[4] < 2) continue; std::vector<unsigned int> matches; // build all combinations and remove any squares we encounter along the way for (auto one : dice1) { // 6 is 9 (upside down) if (one == 9) one = 6; for (auto two : dice2) { // 6 is 9 (upside down) if (two == 9) two = 6; for (auto three : dice3) { // 6 is 9 (upside down) if (three == 9) three = 6; unsigned int current[AllDices] = { one, two, three }; // std::sort is much slower for such small containers if (current[0] > current[1]) std::swap(current[0], current[1]); if (current[1] > current[2]) std::swap(current[1], current[2]); if (current[0] > current[1]) std::swap(current[0], current[1]); auto sortedSquare = 100 * current[0] + 10 * current[1] + current[2]; // if successful then another square number was matched auto match = std::find(squares.begin(), squares.end(), sortedSquare); // remove it from the list if (match != squares.end()) matches.push_back(sortedSquare); } } } if (matches.size() < squares.size()) continue; std::sort(matches.begin(), matches.end()); auto last = std::unique(matches.begin(), matches.end()); open = squares; for (auto m = matches.begin(); m != last; m++) { auto match = std::find(open.begin(), open.end(), *m); open.erase(match); } // all squares matched ? if (open.empty()) valid++; } while (std::next_permutation(permutationDice3.begin(), permutationDice3.end())); } while (std::next_permutation(permutationDice2.begin(), permutationDice2.end())); } while (std::next_permutation(permutationDice1.begin(), permutationDice1.end())); std::cout << valid; return 0; }
This solution contains 28 empty lines, 32 comments and 3 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in 0.01 seconds on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
March 19, 2017 submitted solution
May 9, 2017 added comments
Hackerrank
see https://www.hackerrank.com/contests/projecteuler/challenges/euler090
My code solves 34 out of 43 test cases (score: 77.5%)
I failed 0 test cases due to wrong answers and 9 because of timeouts
Difficulty
Project Euler ranks this problem at 40% (out of 100%).
Hackerrank describes this problem as easy.
Note:
Hackerrank has strict execution time limits (typically 2 seconds for C++ code) and often a much wider input range than the original problem.
In my opinion, Hackerrank's modified problems are usually a lot harder to solve. As a rule thumb: brute-force is rarely an option.
Links
projecteuler.net/thread=90 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
C# www.mathblog.dk/project-euler-90-cubes-make-square/ (written by Kristian Edlund)
C# github.com/HaochenLiu/My-Project-Euler/blob/master/090.cs (written by Haochen Liu)
Python github.com/nayuki/Project-Euler-solutions/blob/master/python/p090.py (written by Nayuki)
Python github.com/roosephu/project-euler/blob/master/90.py (written by Yuping Luo)
Python github.com/steve98654/ProjectEuler/blob/master/090.py
C++ github.com/Meng-Gen/ProjectEuler/blob/master/90.cc (written by Meng-Gen Tsai)
Java github.com/nayuki/Project-Euler-solutions/blob/master/java/p090.java (written by Nayuki)
Java github.com/thrap/project-euler/blob/master/src/Java/Problem90.java (written by Magnus Solheim Thrap)
Go github.com/frrad/project-euler/blob/master/golang/Problem090.go (written by Frederick Robinson)
Scala github.com/samskivert/euler-scala/blob/master/Euler090.scala (written by Michael Bayne)
Perl github.com/gustafe/projecteuler/blob/master/090-Cube-digit-pairs.pl (written by Gustaf Erikson)
Perl github.com/shlomif/project-euler/blob/master/project-euler/90/euler-90.pl (written by Shlomi Fish)
Rust github.com/gifnksm/ProjectEulerRust/blob/master/src/bin/p090.rs
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 | 807 | 808 | 809 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 89 - Roman numerals |

|
Right triangles with integer coordinates - problem 91 >> |