| << problem 359 - Hilbert's New Hotel |

|
Licence plates - problem 371 >> |
Problem 363: Bézier Curves
(see projecteuler.net/problem=363)
A cubic Bézier curve is defined by four points: P_0, P_1, P_2 and P_3.
The curve is constructed as follows:
On the segments P_0 P_1, P_1 P_2 and P_2 P_3 the points Q_0, Q_1 and Q_2 are drawn such that
P_0 Q_0 / P_0 P_1 = P_1 Q_1 / P_1 P_2 = P_2 Q_2 / P_2 P_3 = t (t in [0,1]).
On the segments Q_0 Q_1 and Q_1 Q_2 the points R_0 and R_1 are drawn such that
Q_0 R_0 / Q_0 Q_1 = Q_1 R_1 / Q_1 Q_2 = t for the same value of t.
On the segment R_0 R_1 the point B is drawn such that R_0 B / R_0 R_1 = t for the same value of t.
The Bézier curve defined by the points P_0, P_1, P_2 and P_3 is the locus of B as Q_0 takes all possible positions on the segment P_0 P_1.
(Please note that for all points the value of t is the same.)
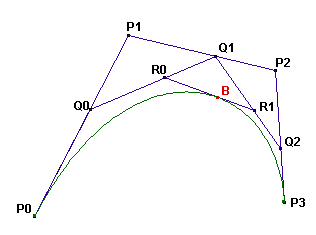
At this (external) web address you will find an applet that allows you to drag the points P_0, P_1, P_2 and P_3
to see what the Bezier curve (green curve) defined by those points looks like.
You can also drag the point Q_0 along the segment P_0 P_1.
From the construction it is clear that the Bézier curve will be tangent to the segments P_0 P_1 in P_0 and P_2 P_3 in P_3.
A cubic Bézier curve with P_0=(1,0), P_1=(1,v), P_2=(v,1) and P_3=(0,1) is used to approximate a quarter circle.
The value v > 0 is chosen such that the area enclosed by the lines O P_0, O P_3 and the curve is equal to pi/4 (the area of the quarter circle).
By how many percent does the length of the curve differ from the length of the quarter circle?
That is, if L is the length of the curve, calculate 100 * dfrac{L - pi/2}{pi/2}
Give your answer rounded to 10 digits behind the decimal point.
My Algorithm
I implemented a generic bezier() function which returns a 2D point interpolated between four Bézier points.
It relies on the deCasteljau algorithm (see en.wikipedia.org/wiki/De_Casteljau's_algorithm).
A bit more accurate and much faster is bezierArc which assumes that the four Bézier points are (1, 0), (1, v), (v, 1), (0, 1).
When these four points are substituted in the formulas for cubic Bézier curves (see en.wikipedia.org/wiki/Bézier_curve#Cubic_B.C3.A9zier_curves) then they simplify to:
(1) B(t) = (1-t)^3 P_0 + 3(1-t)^2 t P_1 + 3(1-t) t^2 P_2 + t^3 P_3
(2) x(t) = (1 - t)^3 + 3(1-t)^2t + 3(1-t) t^2 v
(3) y(t) = 3(1-t)^2tv + 3(1-t) t^2 + t^3
v is unknown and 0 <= t <= 1.
My program initially assumes that v = 0.5 and tries to gradually improve that value (see #ifdef FIND_V):
- a loop iterates t from zero to one with
StepT = 0.000001(that's a million steps) - the resulting area of the Bézier curve is compared against the area of the quarter circle
- if the Bézier curve's area is smaller then v is slightly incremented (and if the area is too big then v is decremented)
But no matter what I tried, I got pretty close but couldn't solve this problem. I couldn't find a better result than a 0.000000122206% deviation from the quarter circle which is wrong.
(if you optimize the constants
StepT and AreaAccuracy you might find slightly better value but most likely not the correct one).Then I went down the dirty road and asked Wolfram Alpha to solve the integral integral{y * dfrac{\delta x}{\delta t} dt} = dfrac{pi}{4}
www.wolframalpha.com/input/?i=Integrate[(3(1-t)^2tv+3(1-t)t^2+t^3) D[(1-t)^3+3(1-t)^2t+3((1-t)t^2v),t], {t, 0, 1}] = pi/4
It displayed
(4) -dfrac{3v^2}{20}+dfrac{3v}{5}+dfrac{1}{2}=dfrac{pi}{4}
(5) v = 2 \pm sqrt{dfrac{22 - 5 pi}{3}}
There are two solutions for v. One is pretty close to what my program converged to, the other solution is far, far away and can be ignored:
v_1 = 3.448221522195532282154562592704972836349668711
v_2 = 0.551778477804467717845437407295027163650331289 → that matches my approximation 0.5517813930
I tried to continue with Wolfram Alpha but lost interest when I saw the weird integrals generated by it.
Nevertheless, those were my ideas (for the sake of completeness):
Wikipedia tells me that the length L of an arc is (see en.wikipedia.org/wiki/Arc_length):
(6) L = integral{1 + (dfrac{dy}{dx})^2} dx
Equations (2) and (3) together with the exact result (v_2):
(7) x(t) = (1 - t)^3 + 3(1-t)^2t + 3(1-t) t^2 (2 - sqrt{dfrac{22 - 5 pi}{3}})
(8) y(t) = 3(1-t)^2t (2 - sqrt{dfrac{22 - 5 pi}{3}}) + 3(1-t) t^2 + t^3
As mentioned before, Wolfram Alpha will find the correct result.
Well, back to my solution:
using the correct v I can recursively compute the length of the Bézier curve using an epsilon:
getLength()computes the length of a line between v_{from} and v_{to}- then it computes the sum of the lengths of the two lines v_{from},v_{(from+to)/2} and v_{(from+to)/2},v_{to}
- if the sum of those two shorter lines differs more than
epsilonfrom the original line then I recursively compute a more accurate length of those two shorter lines
epsilon (I settled with 10^-17).
Alternative Approaches
Meng-Gen Tsai solved the whole problem with Wolfram Alpha despite all the ugly integrals.
I could have integrated equations (7) and (8) numerically (instead of writing getLength()).
Note
There is no live test.
My personal view on this problem: I have a background in Computer Graphics and really like Bézier curves.
After having solved this weird problem, I'm not sure whether I still like Bézier curves anymore.
This problem changed a conceptually very simple technique (especially the very elegant de Casteljau's algorithm) into something full of meaningless integrals.
It took all the beauty out of it. That's sad !
Interactive test
This feature is not available for the current problem.
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
#include <iostream> #include <iomanip> #include <cmath> typedef double Number; // changing it to long double gives the same results // 2D point
struct Point { // create a new point Point(Number x_, Number y_) : x(x_), y(y_) {} // return distance between two points Number distance(const Point& other) const { auto diffX = x - other.x; auto diffY = y - other.y; return sqrt(diffX * diffX + diffY * diffY); } Number x, y; }; // interpolate between four points p0, p1, p2, p3 with parameter t
Point bezier(const Point& p0, const Point& p1, const Point& p2, const Point& p3, Number t) { // see https://en.wikipedia.org/wiki/De_Casteljau%27s_algorithm // linear interpolation between p0 and p1, p1 and p2, p2 and p3 Point q0(p0.x + (p1.x - p0.x) * t, p0.y + (p1.y - p0.y) * t); Point q1(p1.x + (p2.x - p1.x) * t, p1.y + (p2.y - p1.y) * t); Point q2(p2.x + (p3.x - p2.x) * t, p2.y + (p3.y - p2.y) * t); // rinse and repeat: linear interpolation between q0 and q1, q1 and q2 Point r0(q0.x + (q1.x - q0.x) * t, q0.y + (q1.y - q0.y) * t); Point r1(q1.x + (q2.x - q1.x) * t, q1.y + (q2.y - q1.y) * t); // and finally: linear interpolation between q0 and q1, q1 and q2 Point b(r0.x + (r1.x - r0.x) * t, r0.y + (r1.y - r0.y) * t); return b; } // same as bezier() but optimized for the case (1, 0), (1, v), (v, 1), (0, 1)
Point bezierArc(Number v, Number t) { // direct computation of cubic Bezier curves (see https://en.wikipedia.org/wiki/B%C3%A9zier_curve ): // replace p0,p1,p2,p3 by their known values 0, 1 or v return Point(pow(1 - t, 3) + 3*pow(1 - t, 2)*t + 3*(1 - t)*t*t*v, 3*pow(1 - t, 2)*t*v + 3*(1 - t)*t*t + t*t*t); } // find length of Bezier curve between t=from and t=to with an accuracy=epsilon
Number getLength(Number v, Number from, Number to, Number epsilon) { // compute three points: start, middle and end auto bisect = (from + to) / 2; auto start = bezierArc(v, from); auto middle = bezierArc(v, bisect); auto end = bezierArc(v, to); // compute distance start,end against start,middle + middle,end auto totalDistance = start.distance(end); auto firstHalf = middle.distance(start); auto secondHalf = middle.distance(end); auto morePrecise = firstHalf + secondHalf; // enough accuracy ? if (morePrecise < totalDistance + epsilon) return morePrecise; // go deeper, compute start,middle + start,end more accurately return getLength(v, from, bisect, epsilon) + getLength(v, bisect, to, epsilon); } int main() { std::cout << std::fixed << std::setprecision(10); // some pi-based constants const Number pi = 3.14159265358979323846264338327950288419; // expected length of the arc const Number piDiv2 = pi / 2; // find v Number v = 0.5; //#define FIND_V
#ifdef FIND_V // expected area inside the arc const Number piDiv4 = pi / 4; // carefully adjust tolerance thresholds const Number AreaAccuracy = 0.0000000001; const Number StepT = 0.000001; // initial adjustment of v, will become smaller after a few iterations Number step = 0.01; // true when adding "step" to "v", false when subtracting bool increment = true; while (fabs(area - piDiv4) > AreaAccuracy) { Point last(1,0); Number area = 0; for (Number t = 0; t <= 1; t += StepT) { //Point p0(1, 0); //Point p1(1, v); //Point p2(v, 1); //Point p3(0, 1); //auto current = bezier(p0, p1, p2, p3, t); // optimized (=> faster) code auto current = bezierArc(v, t); // "last" is on the right side of "current": last.x > current.x auto diffX = last.x - current.x; auto diffY = last.y - current.y; area += current.y * diffX; last = current; } // reduce deviation by adjusting v if (area < piDiv4) { // change direction ? reduce "step" if (!increment) { step /= 2; increment = true; } // increase v v += step; } else { // change direction ? reduce "step" if (increment) { step /= 2; increment = false; } // decrease v v -= step; } } std::cout << "v=" << v << std::endl; #endif // pretty exact value of v v = 0.551778477804467717845437407295027163650331289; // compute length of the arc auto epsilon = 0.00000000000000001; // found manually (I tried several values until error stabilized) auto length = getLength(v, 0, 1, epsilon); auto error = 100 * (length - piDiv2) / piDiv2; std::cout << error << std::endl; return 0; }
This solution contains 26 empty lines, 38 comments and 5 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in 0.16 seconds on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
September 7, 2017 submitted solution
September 7, 2017 added comments
Difficulty
Project Euler ranks this problem at 35% (out of 100%).
Links
projecteuler.net/thread=363 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
C github.com/LaurentMazare/ProjectEuler/blob/master/e363.c (written by Laurent Mazare)
Java github.com/thrap/project-euler/blob/master/src/Java/Problem363.java (written by Magnus Solheim Thrap)
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 | 807 | 808 | 809 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 359 - Hilbert's New Hotel |

|
Licence plates - problem 371 >> |