| << problem 235 - An Arithmetic Geometric sequence |

|
Twenty-two Foolish Primes - problem 239 >> |
Problem 237: Tours on a 4 x n playing board
(see projecteuler.net/problem=237)
Let T(n) be the number of tours over a 4 * n playing board such that:
- The tour starts in the top left corner.
- The tour consists of moves that are up, down, left, or right one square.
- The tour visits each square exactly once.
- The tour ends in the bottom left corner.
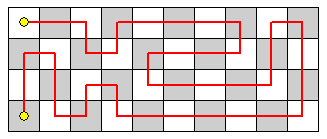
T(10) is 2329. What is T(10^12) mod 10^8?
My Algorithm
A nice problem that you can easily understand within a few seconds. But it took a few days to come up with a solution ...
Of course I immediately wrote a bruteForce algorithm and it solves the T(10) case. Anything beyond that is impossible.
The main realization was to split the whole board in its columns.
I identified 15 different columns (A - O) which can have a unique "flow" on their left and right border.
The term "flow" means the chronological way how a piece moves across the board.
The arrows symbolize the "flow" in and out of a column while hash signs stand for "no border crossing":
ABCDE
→ →→ →→ →→ →→ ##
← ←← #### ←← ←← ##
→ →→ #### →→ ##→ →
← ←← ←← ←← ##← ←
FGHIJ
→ →## →→ #### →→ →
← ←## ←## →→ ##← ##
## →→ →## ←← #### ##
## ←← ←← #### ←## ←
KLMNO
→ ##→ →## →→ ##→ ##
## #### ←## ##← #### ##
## →## ##→ ##→ #### ##
← ←← ##← ←← ##← ##
Columns N and O can only be found at the right edge of the board.
Unfortunately it's not sufficient to represent the flow by arrows because they are still ambigious:
there are three different chronological orders how the "flow" can pass through column A.
If I look at each column's left and right border then there are just 6 patterns for these borders.
With a proper labelling of the flow's chronological order (indicated by 1,2,3,4 and a hash means "no crossing") I get 8 different borders:
111##13#
#221#42#
##32131#
2#4#224#
The function fill() stores the borders of each column, e.g. column C is
neighbors.insert( { "1##2", "1234" } );
Trust me, getting all this stuff right was a lot of work: I made tons of mistakes !
I wrote two algorithms: a simple one that verifies T(10) and a much faster one to solve T(10^12).
slow() linearly goes through all borders that are allowed on the right side of the current border and stops if it reaches the right side of the board.
Assuming that there are about 3 borders that are compatible in such a way, the routine analyzes 3^width combinations.
There's no way it can solve T(10^12) - but I really needed this algorithm to get my borders right.
When the output finally matched the results of bruteForce I went on to write a faster (and more complex) algorithm.
fast() is a divide-and-conquer approach:
- I treat a group of columns as a blackbox where I only knows its left and right border
- if I cut through this blackbox at an arbitrary point then any of the 8 borders could be found
- well, that's not quite right, since the 8th border is reserved for the right-most border of the board → only 7 borders "inside" the blackbox
- then the number of combinations of a blackbox is the product of its left and right half
- if I keep doing this until the blackbox contains only a single column then I check whether this type of column is valid
slow() does ... but when the blackbox becomes smaller, I process the same kinds of blackboxes over and over again.Thus memoization drastically reduced the number of different blackboxes. At the end,
cache contains 3417 values.
Alternative Approaches
I was blown away by the simple solutions found by others: they discovered a relationship between T(n) and T(n-1), ..., T(n-4).
Incredible stuff - or maybe just looked up in OEIS A181688.
Note
Even though the result is found within about 0.02 seconds, I felt that dividing each blackbox in the middle isn't optimal:
if I try to divide the blackbox in such a way that at least one half's size is a power of two (that means 2^i) then cache contains only 2031 values.
Moreover, the program runs about 50% faster.
Replacing the std::string by plain integers would be still faster but I think it would be much harder to understand the code.
Interactive test
You can submit your own input to my program and it will be instantly processed at my server:
This is equivalent toecho 10 | ./237
Output:
Note: the original problem's input 1000000000000 cannot be entered
because just copying results is a soft skill reserved for idiots.
(this interactive test is still under development, computations will be aborted after one second)
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
#include <iostream> #include <set> #include <map> #include <vector> #include <tuple> // assuming that the route could exceed the left border I get these states for the left-most and right-most borders:
typedef std::string Border; const Border LeftBorder = "1##2"; const Border RightBorder = "####"; // all possible borders that can be found inside the grid
std::set<Border> borders; // define which borders can be next to each other
std::set<std::pair<Border, Border>> neighbors; // set up the containers "borders" and "neighbors"
void fill() { // the following lines are derived from my drawings above // left right column neighbors.insert( { "1234", "1234" } ); // A neighbors.insert( { "1432", "1432" } ); // A neighbors.insert( { "3214", "3214" } ); // A neighbors.insert( { "1432", "1##2" } ); // B neighbors.insert( { "3214", "1##2" } ); // B neighbors.insert( { "1##2", "1234" } ); // C neighbors.insert( { "1234", "12##" } ); // D neighbors.insert( { "1234", "##12" } ); // E neighbors.insert( { "12##", "1432" } ); // F neighbors.insert( { "##12", "3214" } ); // G neighbors.insert( { "1##2", "#12#" } ); // H neighbors.insert( { "#12#", "1##2" } ); // I neighbors.insert( { "12##", "1##2" } ); // J neighbors.insert( { "1##2", "##12" } ); // K neighbors.insert( { "1##2", "12##" } ); // L neighbors.insert( { "##12", "1##2" } ); // M neighbors.insert( { "1234", RightBorder } ); // N neighbors.insert( { "1##2", RightBorder } ); // O for (auto x : neighbors) borders.insert(x.first); } // fast search in O(log n)
unsigned long long search(const Border& left, const Border& right, unsigned long long length, unsigned int modulo) { // reduced to a single column ? if (length == 1) // can these two borders be next to each other ? return neighbors.count(std::make_pair(left, right)); // memoize auto id = std::make_tuple(left, right, length); // I don't add "modulo" to the key to keep it simple static std::map<std::tuple<Border, Border, unsigned long long>, unsigned long long> cache; auto lookup = cache.find(id); if (lookup != cache.end()) return lookup->second; // split region into two parts: every possible border can be at the splitting point unsigned long long result = 0; for (const auto& next : borders) { // prefer a "power of two"-splitting, causes less states than splitting 50:50 unsigned long long pow2 = 1; while (pow2 < length / 2) pow2 *= 2; //pow2 = length / 2; // alternatively: less efficient 50:50 method // process left half auto leftHalf = search(left, next, pow2, modulo); // process right half auto rightHalf = search(next, right, length - pow2, modulo); // each left half can be combined with each right half auto combined = (leftHalf * rightHalf) % modulo; result += combined; } result %= modulo; cache[id] = result; return result; } // slow search, no caching whatsoever
unsigned long long slow(const std::string& border, unsigned int length, unsigned int width, unsigned int modulo) { // walked across the whole board ? if (length == width) return (border == RightBorder) ? 1 : 0; // proceed with each border that is compatible to the current one unsigned long long result = 0; for (auto x : neighbors) if (x.first == border) result += slow(x.second, length + 1, width, modulo); return result % modulo; } // backtracking of possible paths, doesn't need the information about borders etc.
typedef std::vector<std::vector<unsigned int>> Grid; unsigned int bruteForce(Grid& grid, unsigned int x, unsigned int y, unsigned int step) { // reached final position ? if (x == 0 && y == 3) return (step == grid.size() * grid[0].size()) ? 1 : 0; // take a step grid[x][y] = step; // try to search deeper in each direction unsigned int result = 0; if (x > 0 && grid[x - 1][y] == 0) result += bruteForce(grid, x - 1, y, step + 1); if (x + 1 < grid.size() && grid[x + 1][y] == 0) result += bruteForce(grid, x + 1, y, step + 1); if (y > 0 && grid[x][y - 1] == 0) result += bruteForce(grid, x, y - 1, step + 1); if (y < 3 && grid[x][y + 1] == 0) result += bruteForce(grid, x, y + 1, step + 1); // undo step grid[x][y] = 0; return result; } int main() { // set up borders and their relationships fill(); unsigned int modulo = 100000000; unsigned long long limit = 1000000000000; std::cin >> limit; //#define BRUTEFORCE
#ifdef BRUTEFORCE // allocate memory Grid grid(limit); for (auto& column : grid) column.resize(4, 0); // start in upper left corner (0,0), that's the first step std::cout << bruteForce(grid, 0, 0, 1) << std::endl; #endif //#define SLOW
#ifdef SLOW std::cout << slow(LeftBorder, 0, limit, modulo) << std::endl; #endif #define FAST #ifdef FAST std::cout << search(LeftBorder, RightBorder, limit, modulo) << std::endl; #endif return 0; }
This solution contains 24 empty lines, 30 comments and 12 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in 0.01 seconds on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
October 17, 2017 submitted solution
October 17, 2017 added comments
Difficulty
Project Euler ranks this problem at 70% (out of 100%).
Links
projecteuler.net/thread=237 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
Python github.com/LaurentMazare/ProjectEuler/blob/master/e237.py (written by Laurent Mazare)
Python github.com/roosephu/project-euler/blob/master/237.py (written by Yuping Luo)
Python github.com/smacke/project-euler/blob/master/python/237.py (written by Stephen Macke)
Java github.com/thrap/project-euler/blob/master/src/Java/Problem237.java (written by Magnus Solheim Thrap)
Go github.com/frrad/project-euler/blob/master/golang/Problem237.go (written by Frederick Robinson)
Perl github.com/shlomif/project-euler/blob/master/project-euler/237/euler-237-v1.pl (written by Shlomi Fish)
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 | 807 | 808 | 809 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 235 - An Arithmetic Geometric sequence |

|
Twenty-two Foolish Primes - problem 239 >> |