| << problem 188 - The hyperexponentiation of a number |

|
Maximising a weighted product - problem 190 >> |
Problem 189: Tri-colouring a triangular grid
(see projecteuler.net/problem=189)
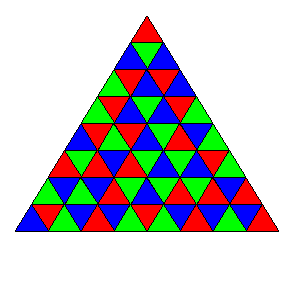
Consider the following configuration of 64 triangles:

We wish to colour the interior of each triangle with one of three colours: red, green or blue, so that no two neighbouring triangles have the same colour. Such a colouring shall be called valid. Here, two triangles are said to be neighbouring if they share an edge.
Note: if they only share a vertex, then they are not neighbours.
For example, here is a valid colouring of the above grid:
A colouring C' which is obtained from a colouring C by rotation or reflection is considered distinct from C unless the two are identical.
How many distinct valid colourings are there for the above configuration?
My Algorithm
I solved this problem in classic Dynamic Programming way:
- generate each possible row triangle-by-triangle, beginning with the top row
- whenever I start a new row check if I already fully processed a row similar to the most previous row
For example, each color of the top-most triangle is similar to each other because I can permute the color such that I can produce the original coloring.
My function
getId() returns a hash value of a row stored in triangle. If two rows share the same hash then they must be similar.Only a row's triangles that share an edge with the row beneath it are relevant (in general: each triangle with an even index).
In the third row of the example, only the left-most green and the two blue triangles have to be considered by
getId().Each color is represented by an integer: Red = 1, Green = 2, Blue = 3.
Initially I used these codes to get a hash value
id = row * (color[0] * 3^0 + color[2] * 3^1 + color[4] * 3^2 * ...)
Then it occurred to me that the differences between those relevant triangles are sufficient (plus 3 if difference is negative):
id = row * ((color[2] - color[0]) * 3^0 + (color[4] - color[2]) * 3^1 + (color[6] - color[4]) * 3^2 + ...)
Due to symmetry, each row is similar to itself when all relevant triangles are in reverse order (see
#define SYMMETRIC_ID).So I compute two hashes and choose the smaller one because I want to have as many rows as possible to share the same hash value / ID.
Alternative Approaches
There is something called "chromatic polynomials" which can solve this problem, too (see en.wikipedia.org/wiki/Chromatic_polynomial).
I haven't tried it but it seems to be a faster way.
Modifications by HackerRank
The number of colors can be larger than 3 and the maximum height of the triangle is 11.
My solution times out for about every fifth test case.
Interactive test
You can submit your own input to my program and it will be instantly processed at my server:
This is equivalent toecho "4 3" | ./189
Output:
Note: the original problem's input 8 3 cannot be entered
because just copying results is a soft skill reserved for idiots.
(this interactive test is still under development, computations will be aborted after one second)
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
The code contains #ifdefs to switch between the original problem and the Hackerrank version.
Enable #ifdef ORIGINAL to produce the result for the original problem (default setting for most problems).
#include <iostream> #include <vector> #include <map> #define ORIGINAL // disable for Hackerrank #define SYMMETRIC_ID // identify rows in reverse order as similar // total height
unsigned int height = 8; unsigned int numColors = 3; // "scratchpad", used while processing the colorings
typedef char Color; std::vector<Color> triangles; // cache result for completed rows, index is determined by getId()
#ifdef ORIGINAL std::vector<unsigned long long> cache(5102 + 1, 0); // sufficient for height<=8 and numColors<=3 #else std::map<unsigned int, unsigned long long> cache; // handle bigger input values, too #endif // compute hash value of a row
unsigned int getId(unsigned int row) { auto first = row * row; auto width = 2 * row + 1; // compute hash of triangles: find differences between adjacent triangles of the same orientation unsigned int result = row; for (auto i = first + 2; i < first + width; i += 2) { auto diff = triangles[i - 2] - triangles[i]; if (diff < 0) diff += numColors; result = result * numColors + diff; } #ifdef SYMMETRIC_ID // simple optimization based on symmetry: process the same triangles in reverse order: unsigned int reverse = row; for (auto i = first + width - 1; i >= first + 2; i -= 2) { // exactly the same as above but "i" is running in reverse auto diff = triangles[i - 2] - triangles[i]; if (diff < 0) diff += numColors; reverse = reverse * numColors + diff; } if (result > reverse) result = reverse; #endif return result; } // simple enumeration, solves triangle with 5 rows in about a second
unsigned long long search(unsigned int row = 0, unsigned int column = 0) { // index of the first triangle in the current row auto first = row * row; // index of the current triangle auto index = first + column; // number of triangles in the current row auto width = 2 * row + 1; // "coordinates" of the next triangle auto nextRow = row; auto nextColumn = column + 1; if (nextColumn == width) { // start a new row nextRow++; nextColumn = 0; } // hash value of the previous row, only needed when starting a new row unsigned int prevId = 0; if (column == 0) { // finished ? if (row == height) return 1; // found another valid coloring if (row == 0) cache.clear(); // only relevant when computing multiple triangle sizes (as I did while developing my solution) else // row > 0 { // already cached ? prevId = getId(row - 1); if (cache[prevId] != 0) return cache[prevId]; } } // recursively process current position unsigned long long result = 0; if (column % 2 == 0) // even: no contact to triangle in row above for (Color color = 1; color <= (Color)numColors; color++) { // exclude color of left neighbor (but first triangle in a row can have any color because it has no left neighbor) if (column > 0 && triangles[index - 1] == color) continue; triangles[index] = color; result += search(nextRow, nextColumn); } else // odd: must respect triangle in row above for (Color color = 1; color <= (Color)numColors; color++) { // exclude color of left neighbor and neighbor in row above if (triangles[index - 1] == color || triangles[index - 2 * row] == color) continue; triangles[index] = color; result += search(nextRow, nextColumn); } #ifndef ORIGINAL // Hackerrank only result %= 1000000007; #endif // store result if (column == 0 && row > 0) cache[prevId] = result; return result; } int main() { std::cin >> height >> numColors; triangles.resize(height * height); // let's go ! std::cout << search() << std::endl; return 0; }
This solution contains 20 empty lines, 22 comments and 12 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in 0.03 seconds on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
September 5, 2017 submitted solution
September 5, 2017 added comments
Hackerrank
see https://www.hackerrank.com/contests/projecteuler/challenges/euler189
My code solves 72 out of 91 test cases (score: 78.89%)
I failed 0 test cases due to wrong answers and 19 because of timeouts
Difficulty
Project Euler ranks this problem at 70% (out of 100%).
Hackerrank describes this problem as easy.
Note:
Hackerrank has strict execution time limits (typically 2 seconds for C++ code) and often a much wider input range than the original problem.
In my opinion, Hackerrank's modified problems are usually a lot harder to solve. As a rule thumb: brute-force is rarely an option.
Links
projecteuler.net/thread=189 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
Python github.com/LaurentMazare/ProjectEuler/blob/master/e189.py (written by Laurent Mazare)
Python github.com/Meng-Gen/ProjectEuler/blob/master/189.py (written by Meng-Gen Tsai)
C++ github.com/roosephu/project-euler/blob/master/189.cpp (written by Yuping Luo)
Java github.com/HaochenLiu/My-Project-Euler/blob/master/189.java (written by Haochen Liu)
Java github.com/thrap/project-euler/blob/master/src/Java/Problem189.java (written by Magnus Solheim Thrap)
Go github.com/frrad/project-euler/blob/master/golang/Problem189.go (written by Frederick Robinson)
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 | 807 | 808 | 809 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 188 - The hyperexponentiation of a number |

|
Maximising a weighted product - problem 190 >> |