| << problem 310 - Nim Square |

|
Digital root clocks - problem 315 >> |
Problem 313: Sliding game
(see projecteuler.net/problem=313)
In a sliding game a counter may slide horizontally or vertically into an empty space.
The objective of the game is to move the red counter from the top left corner of a grid to the bottom right corner;
the space always starts in the bottom right corner.
For example, the following sequence of pictures show how the game can be completed in five moves on a 2 by 2 grid.
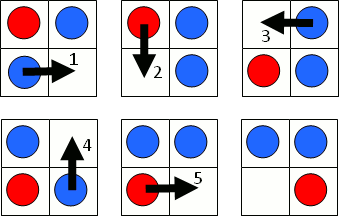
Let S(m,n) represent the minimum number of moves to complete the game on an m by n grid. For example, it can be verified that S(5,4) = 25.
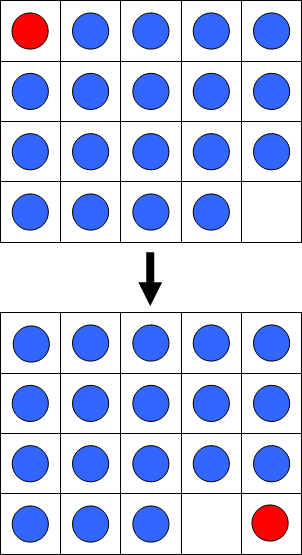
There are exactly 5482 grids for which S(m,n) = p^2, where p < 100 is prime.
How many grids does S(m,n) = p^2, where p < 10^6 is prime?
My Algorithm
Wow, I needed quite some time to solve this apparently easy problem (difficulty rated at just 30% by Project Euler) ...
These three steps were taken:
1. write a simple brute-force solution for very small m and n
2. deduce a slightly smarter version for S(m,n) = p^2 where p < 100
3. find the the fast formula for p < 10^6
bruteForce() represents my first step: it's a breadth-first search that generates all "moves" of the empty square until the red counter is in its final position.
Even though a substantial amount of code is devoted to this algorithm, it is pretty straightforward and easy to implement (and I enjoyed it !).
It pretty obvious that S(m, n) = S(n, m). Therefore I assume in the following text that m >= n.
I printed the results for n <= m <= 15 and observed a pattern which lead to the faster search() (my second step):
(1) S(m, 2) = S(m-1, 2) + 6
(2) S(m, n) = S(m, n-1) + 2
There are a few exceptions: S(2, 2) = 0 and S(3, 2) = 9 and S(3, 3) = 13.
It took a few minutes to get everything right and, voila !, search() found the correct result 5482 for p < 100.
The problem asks for p < 10^6 which is 10^4 times larger - and due to the quadratic nature of my algorithm it will take about 10^8 as long. That's several days !
After a few days I revisited my partial solution and further analyzed my debugging output and again, there was a pattern:
the differences between consecutive numbers grow almost quadratic:
pp^2S_pdiff = S_p - S_{p-1}p^2 / diff
392
525424.5
7498412.5
11121181012.25
13169321412.1
17289562412.07143...
19361863012.04167...
235291304412.03333...
298412007012.02273...
The last column gets closer and closer to 12 !
I tried a few formulas in a spreadsheet and it turns out that diff = (p^2 - 1) / 12 matches all cases except for p = 3.
My final algorithm is to compute the sum of (p^2 - 1) / 12 for all primes p (except for p = 3 then it's 2).
Note
I couldn't find an obvious mathematical approach and solved this with a combination of programming and lots of guesswork.
That's not desirable - well, I like the programming part but guessing isn't my strong suit.
Admittedly, the final algorithm is very simple and could be considered "worth" only 30% but it's not an easy way to get there.
I had to write more than 200 lines of code to "stumble upon" a one-liner solution.
Interactive test
You can submit your own input to my program and it will be instantly processed at my server:
This is equivalent toecho 100 | ./313
Output:
Note: the original problem's input 1000000 cannot be entered
because just copying results is a soft skill reserved for idiots.
(this interactive test is still under development, computations will be aborted after one second)
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
#include <iostream> #include <vector> #include <set> #include <cmath> // ---------- standard prime sieve from my toolbox ----------
// odd prime numbers are marked as "true" in a bitvector
std::vector<bool> sieve; // return true, if x is a prime number
bool isPrime(unsigned int x) { // handle even numbers if ((x & 1) == 0) return x == 2; // lookup for odd numbers return sieve[x >> 1]; } // find all prime numbers from 2 to size
void fillSieve(unsigned int size) { // store only odd numbers const unsigned int half = (size >> 1) + 1; // allocate memory sieve.resize(half, true); // 1 is not a prime number sieve[0] = false; // process all relevant prime factors for (unsigned int i = 1; 2*i*i < half; i++) // do we have a prime factor ? if (sieve[i]) { // mark all its multiples as false unsigned int current = 3*i+1; while (current < half) { sieve[current] = false; current += 2*i+1; } } } // ---------- problem specific code ----------
// (0,0) is located in the upper-left corner
struct Board { typedef unsigned int Number; // position of the red counter Number redX, redY; // empty square Number emptyX, emptyY; Board(Number redX_, Number redY_, Number emptyX_, Number emptyY_) : redX(redX_), redY(redY_), emptyX(emptyX_), emptyY(emptyY_) {} // for std::set bool operator<(const Board& other) const { if (redX != other.redX) return redX < other.redX; if (redY != other.redY) return redY < other.redY; if (emptyX != other.emptyX) return emptyX < other.emptyX; return emptyY < other.emptyY; } }; // breadth-search
unsigned int bruteForce(unsigned int width, unsigned int height) { // ensure width >= height if (width < height) std::swap(width, height); // start with the red counter in the upper-left corner and empty square in lowe-right corner Board initial(0,0, width-1,height-1); std::vector<Board> todo = { initial }; std::set<Board> visited = { initial }; unsigned int depth = 0; while (!todo.empty()) { std::vector<Board> next; for (auto current : todo) { // finished ? if (current.redX == width - 1 && current.redY == height - 1) return depth; // "move" the empty square, ignore already visited positions // right if (current.emptyX + 1 < width) { Board right = current; right.emptyX++; // move red counter ? if (right.emptyX == right.redX && right.emptyY == right.redY) right.redX--; // if unvisited yet, then add to queue for next iteration if (visited.count(right) == 0) { next.push_back(right); visited.insert(right); } } // left if (current.emptyX > 0) { Board left = current; left.emptyX--; // move red counter ? if (left.emptyX == left.redX && left.emptyY == left.redY) left.redX++; // if unvisited yet, then add to queue for next iteration if (visited.count(left) == 0) { next.push_back(left); visited.insert(left); } } // down if (current.emptyY + 1 < height) { Board down = current; down.emptyY++; // move red counter ? if (down.emptyX == down.redX && down.emptyY == down.redY) down.redY--; // if unvisited yet, then add to queue for next iteration if (visited.count(down) == 0) { next.push_back(down); visited.insert(down); } } // up if (current.emptyY > 0) { Board up = current; up.emptyY--; // move red counter ? if (up.emptyX == up.redX && up.emptyY == up.redY) up.redY++; // if unvisited yet, then add to queue for next iteration if (visited.count(up) == 0) { next.push_back(up); visited.insert(up); } } } // next iteration todo = std::move(next); depth++; } // unsolvable grid return 0; // never reached } // just a bit of pattern matching until it produced the same results as bruteForceSlow()
unsigned int search(unsigned int width, unsigned int height) { // ensure width >= height if (width < height) std::swap(width, height); // small grids are impossible if (width < 2) return 0; // precalculated results for 2x2, 3x2 and 3x3 if (width == 2) return 5; if (width == 3) return height == 2 ? 9 : 13; // result for height = 2 auto two = 6 * width - 9; // and adjust for arbitrary height auto full = two + 2 * height - 4; // two more moves required if both sides are equal if (width == height) full += 2; return full; } int main() { unsigned int limit = 1000000; std::cin >> limit; // verify the two drawings //std::cout << bruteForce(2, 2) << std::endl; //std::cout << bruteForce(5, 4) << std::endl; // generate enough prime numbers fillSieve(limit); //#define VERIFY_100
#ifdef VERIFY_100 // use faster bruteForce() function to verify S(100) for (unsigned int current = 2; current <= limit; current++) { if (!isPrime(current)) continue; unsigned int sum = 0; // verify the larger dataset p^2 where p is a prime and p < 100 for (unsigned int width = 2; search(width, 2) <= current*current; width++) for (unsigned int height = 2; height <= width; height++) { auto steps = search(width, height); // too large ? if (steps > current * current) break; // is it a square of a prime ? unsigned int root = sqrt(steps); if (root * root != steps || !isPrime(root)) continue; // found one more solution sum++; // symmetry: if (m,n) is a solution then (n,m) is a solution, too if (width != height) sum++; } // display result std::cout << "S(" << current << ")=" << sum << std::endl; } #endif // fast algorithm unsigned long long sum = 0; for (unsigned int p = 2; p <= limit; p++) { if (!isPrime(p)) continue; // increment is (p^2 - 1) / 12 // need 64 bit for p^2 auto square = (unsigned long long) p * p; auto increment = (square - 1) / 12; // except if p=3 if (p == 3) sum += 2; else sum += increment; } // finally ... std::cout << sum << std::endl; return 0; }
This solution contains 33 empty lines, 60 comments and 6 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in less than 0.01 seconds on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
September 19, 2017 submitted solution
September 19, 2017 added comments
Difficulty
Project Euler ranks this problem at 30% (out of 100%).
Links
projecteuler.net/thread=313 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
Python github.com/roosephu/project-euler/blob/master/313.py (written by Yuping Luo)
Python github.com/smacke/project-euler/blob/master/python/313.py (written by Stephen Macke)
C++ github.com/evilmucedin/project-euler/blob/master/euler313/euler313.cpp (written by Den Raskovalov)
Java github.com/thrap/project-euler/blob/master/src/Java/Problem313.java (written by Magnus Solheim Thrap)
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 | 807 | 808 | 809 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 310 - Nim Square |

|
Digital root clocks - problem 315 >> |