| << problem 127 - abc-hits |

|
Repunit divisibility - problem 129 >> |
Problem 128: Hexagonal tile differences
(see projecteuler.net/problem=128)
A hexagonal tile with number 1 is surrounded by a ring of six hexagonal tiles, starting at "12 o'clock" and numbering the tiles 2 to 7 in an anti-clockwise direction.
New rings are added in the same fashion, with the next rings being numbered 8 to 19, 20 to 37, 38 to 61, and so on. The diagram below shows the first three rings.
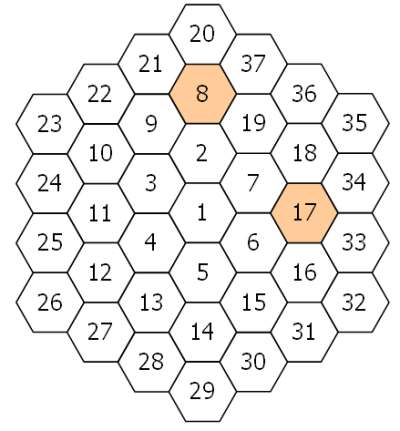
By finding the difference between tile n and each of its six neighbours we shall define PD(n) to be the number of those differences which are prime.
For example, working clockwise around tile 8 the differences are 12, 29, 11, 6, 1, and 13. So PD(8) = 3.
In the same way, the differences around tile 17 are 1, 17, 16, 1, 11, and 10, hence PD(17) = 2.
It can be shown that the maximum value of PD(n) is 3.
If all of the tiles for which PD(n) = 3 are listed in ascending order to form a sequence, the 10th tile would be 271.
Find the 2000th tile in this sequence.
My Algorithm
Tile 1 matches all conditions: PD(1) = 3 because 4-1=3 is prime, 3-1=2 is prime and 6-1=5 is prime.
Tile 2 matches all conditions: PD(2) = 3 because 9-2=7 is prime, 19-2=17 is prime and 7-2=5 is prime.
My first program performed that task for all numbers from 1 to 1000. It didn't find the solution because surprisingly only a tiny fraction of tiles matches all conditions.
Then I looked at tile 17 more closely:
- its predecessor and its successor are neighbors, their difference is 1 which is not a prime
- on its left side (the ring inside) there are the two consecutive numbers 6 and 7. Only one difference is odd, the other is even (can't be a prime)
- on its right side (the ring outside) there are the two consecutive numbers 33 and 34. Only one difference is odd, the other is even (can't be a prime)
In general, every number located on the edge/side of a ring has PD(x) <= 2. Therefore 9, 11, 13, 15, 17, 21, 22, 24, 25, 27, 28, ... can be excluded.
Note that there is a single exception: the last tiles of each ring (7, 19, 37, ...) have no connection to their successors. They remain candidates for PD(x) = 3.
Now only the numbers on the "corners" of each ring are left (such as 2,3,4,5,6,7,8,10,12,14,16,18,20,23,26,...).
Except for the corners "north" of 1 (2,8,20,..., they are the first numbers of a ring), each of those tiles is connected to its predecessor and its successor (remember: difference is 1 → no prime).
The neighbors on the outside ring are three consecutive numbers. Only if the difference to the first and the last of these three tiles is odd, then at most two differences can be prime.
For PD(x)=3, the inner tile must be prime, too. That means either the two relevant outer and the inner tile are odd while the corner tile is even or
the two relevant outer and the inner tile are even while the corner tile is odd.
The inner tile is a corner tile, too, and has the difference 6 * ring + corner (where 1 <= corner <= 5, I look at the "north" tile later).
Clearly, the second and fourth corner have always an even difference and their PD(x) must be smaller than 3.
The middle of the outer three tiles is a corner tile as well and has a difference of 6 * (ring+1) + corner.
Obviously, its predecessor and successor have a difference of 6 * (ring+1) + corner \pm 1.
The first, third and fifth corner produce an even difference which is never prime.
These formulas are a bit off for the first 7 tiles because my formulas 6 * ring and 6 * (ring+1) are valid everywhere - but not in the centre.
I manually inspected the first seven tiles and found that only tiles 1 and 2 match all conditions.
The only tiles left are the first and last tiles of each ring. My program checks their surrounding tiles, or better say, their differences.
The difference between the first tile of the current ring and the first tile of the previous ring is
incrementFrom = (ring - 1) * 6 (where ring denotes the current ring).The difference between the first tile of the current ring and the first tile of the next ring is
incrementTo = ring * 6.And the difference between the first tile of the current ring and the ring beyond the next ring is
incrementTo2 = (ring + 1) * 6 + incrementTo.There are six tiles around the first tile of ring and their differences are (beginning from the bottom at 6 o'clock, 8 o'clock, 10 o'clock, ..., 4 o'clock):
a = incrementFrom → multiple of 6, never primeb = 1 → never primec = incrementTo + 1d = incrementTo → multiple of 6, never primee = incrementTo2 - 1f = incrementTo - 1Only three tiles are actual candidates (
c, e and f).There are six tiles around the last tile of ring and their differences are (same order as first tile):
a = incrementTo → multiple of 6, never primeb = incrementFrom + incrementTo - 1c = incrementTo - 1d = incrementTo2 - incrementTo → multiple of 6, never primee = incrementTo2 - incrementTo - 1f = 1 → never primeOnly three tiles are actual candidates (
b, c and e).One difference appears for both tiles (
incrementTo - 1). My program checks this difference first for a small performance gain.
Note
The upper limit of my prime sieve was determined by running the program a few times and counting which primes where checked
(by the way: I used the Miller-Rabin primality test but it is magnitudes slower than the current primitive sieve).
Interactive test
You can submit your own input to my program and it will be instantly processed at my server:
This is equivalent toecho "1 10" | ./128
Output:
Note: the original problem's input 2000 cannot be entered
because just copying results is a soft skill reserved for idiots.
(this interactive test is still under development, computations will be aborted after one second)
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
The code contains #ifdefs to switch between the original problem and the Hackerrank version.
Enable #ifdef ORIGINAL to produce the result for the original problem (default setting for most problems).
#include <iostream> #include <vector> // standard prime sieve, see my toolbox // odd prime numbers are marked as "true" in a bitvector
std::vector<bool> sieve; // return true, if x is a prime number
bool isPrime(unsigned int x) { // handle even numbers if ((x & 1) == 0) return x == 2; // lookup for odd numbers return sieve[x >> 1]; } // find all prime numbers from 2 to size
void fillSieve(unsigned int size) { // store only odd numbers const unsigned int half = size >> 1; // allocate memory sieve.resize(half, true); // 1 is not a prime number sieve[0] = false; // process all relevant prime factors for (unsigned int i = 1; 2 * i*i < half; i++) // do we have a prime factor ? if (sieve[i]) { // mark all its multiples as false unsigned int current = 3 * i + 1; while (current < half) { sieve[current] = false; current += 2 * i + 1; } } } int main() { // fill a prime sieve (maximum prime was determined by running it a few times) #define ORIGINAL #ifdef ORIGINAL unsigned int limit = 2000; fillSieve(835000); #else unsigned int limit = 80000; fillSieve(91200000); #endif // [nth number] => [tile] std::vector<unsigned long long> found = { 1, 2 }; // tiles 1 and 2 are the first two tiles because PD(1)=PD(2)=3 unsigned int numFound = 2; // and there are no further tiles below 8 where PD(x)=3 unsigned long long first = 8; // analyze rings until enough numbers are found for (unsigned long long ring = 2; numFound < limit; ring++) { // difference to previous ring (inside current ring) auto incrementFrom = (ring - 1) * 6; // difference to next ring (outside current ring) auto incrementTo = ring * 6; // difference to ring after the next ring auto incrementTo2 = (ring + 1) * 6 + incrementTo; // difference "incrementTo - 1" appears twice: around first and last tile if (!isPrime(incrementTo - 1)) { first += incrementTo; continue; } // check first number of a ring if (isPrime(incrementTo + 1) && isPrime(incrementTo2 - 1)) { numFound++; found.push_back(first); } // check last number of a ring if (isPrime(incrementFrom + incrementTo - 1) && isPrime(incrementTo2 - incrementTo - 1)) { numFound++; auto last = first + incrementTo - 1; found.push_back(last); } // next ring first += incrementTo; } // look up results unsigned int tests = 1; std::cin >> tests; while (tests--) { unsigned int index = 2000; std::cin >> index; std::cout << found[index - 1] << std::endl; } return 0; }
This solution contains 17 empty lines, 25 comments and 6 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in less than 0.01 seconds on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
June 24, 2017 submitted solution
June 24, 2017 added comments
Hackerrank
see https://www.hackerrank.com/contests/projecteuler/challenges/euler128
My code solves 9 out of 9 test cases (score: 100%)
Difficulty
Project Euler ranks this problem at 55% (out of 100%).
Hackerrank describes this problem as hard.
Note:
Hackerrank has strict execution time limits (typically 2 seconds for C++ code) and often a much wider input range than the original problem.
In my opinion, Hackerrank's modified problems are usually a lot harder to solve. As a rule thumb: brute-force is rarely an option.
Links
projecteuler.net/thread=128 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
C# www.mathblog.dk/project-euler-128-which-tiles-in-the-hexagonal-arrangement-have-prime-differences-with-neighbours/ (written by Kristian Edlund)
C# github.com/HaochenLiu/My-Project-Euler/blob/master/128.cs (written by Haochen Liu)
Python github.com/nayuki/Project-Euler-solutions/blob/master/python/p128.py (written by Nayuki)
Python github.com/steve98654/ProjectEuler/blob/master/128.py
C++ github.com/Meng-Gen/ProjectEuler/blob/master/128.cc (written by Meng-Gen Tsai)
C++ github.com/roosephu/project-euler/blob/master/128.cpp (written by Yuping Luo)
Java github.com/nayuki/Project-Euler-solutions/blob/master/java/p128.java (written by Nayuki)
Java github.com/thrap/project-euler/blob/master/src/Java/Problem128.java (written by Magnus Solheim Thrap)
Go github.com/frrad/project-euler/blob/master/golang/Problem128.go (written by Frederick Robinson)
Mathematica github.com/nayuki/Project-Euler-solutions/blob/master/mathematica/p128.mathematica (written by Nayuki)
Mathematica github.com/steve98654/ProjectEuler/blob/master/128.nb
Haskell github.com/nayuki/Project-Euler-solutions/blob/master/haskell/p128.hs (written by Nayuki)
Perl github.com/shlomif/project-euler/blob/master/project-euler/128/euler-128.pl (written by Shlomi Fish)
Rust github.com/gifnksm/ProjectEulerRust/blob/master/src/bin/p128.rs
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 | 807 | 808 | 809 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 127 - abc-hits |

|
Repunit divisibility - problem 129 >> |