| << problem 142 - Perfect Square Collection |

|
How many reversible numbers are there below ... - problem 145 >> |
Problem 144: Investigating multiple reflections of a laser beam
(see projecteuler.net/problem=144)
In laser physics, a "white cell" is a mirror system that acts as a delay line for the laser beam.
The beam enters the cell, bounces around on the mirrors, and eventually works its way back out.
The specific white cell we will be considering is an ellipse with the equation 4x^2 + y^2 = 100
The section corresponding to -0.01 <= x <= +0.01 at the top is missing, allowing the light to enter and exit through the hole.
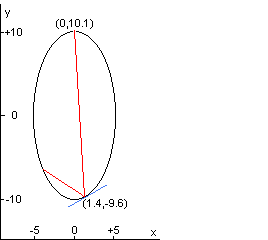
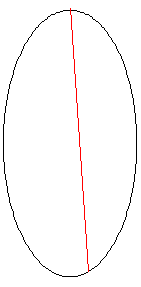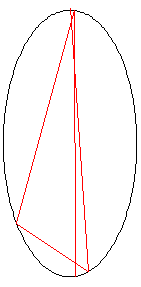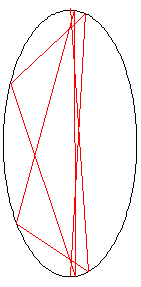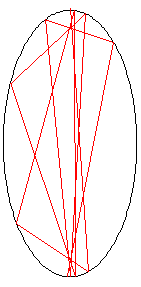
The light beam in this problem starts at the point (0.0,10.1) just outside the white cell, and the beam first impacts the mirror at (1.4,-9.6).
Each time the laser beam hits the surface of the ellipse, it follows the usual law of reflection "angle of incidence equals angle of reflection."
That is, both the incident and reflected beams make the same angle with the normal line at the point of incidence.
In the figure on the left, the red line shows the first two points of contact between the laser beam and the wall of the white cell;
the blue line shows the line tangent to the ellipse at the point of incidence of the first bounce.
The slope m of the tangent line at any point (x,y) of the given ellipse is: m = -4x/y
The normal line is perpendicular to this tangent line at the point of incidence.
The animation on the right shows the first 10 reflections of the beam.
How many times does the beam hit the internal surface of the white cell before exiting?
My Algorithm
I solved this problem using a combination of vector computations and playing with the formula of an ellipse.
The structs Vector and Point are very simple. I could get rid of them and just use simple variables
but I like to have my code clean and organized instead of short and unreadable.
Each iteration of the main loop performs these tasks:
1. check the intersection to whether it belongs to the hole on top of the ellipse (and isn't actually a hole).
2. find the normal at point to
3. reflect the ray's direction in relation to the normal
4. compute next intersection of the new ray
I consider every intersection between -0.01 <= x <= +0.01 and y > 9.9 to be a valid exit point.
(it's even sufficient to ask for y > 0, but don't change the 9.9 to 10 because of the curving of the ellipse).
The reflection can be found very easily with the dot product (nice and short explanation: paulbourke.net/geometry/reflected/)
It took me quite some time to come up with a formula that computes the next intersection.
The ray has a slope s = y / x and any point on the ray is described as
(1) y_2 = s(x_2 - x_1) + y_1
The ellipse was defined as 4x^2 + y^2 = 100 which is
(2) dfrac{x^2}{5} + dfrac{y^2}{10} = 1 (that means a = 5 and b = 10)
The first (already known) intersection occurs at
(3) 4x_1^2 + y_1^2 = 1
The second (unknown) intersection will be at
(4) 4x_2^2 + y_2^2 = 1
I replace in the latter formula (4) the variable y_2 by the ray equation (1):
(5) 4x_2^2 + (s(x_2 - x_1) + y_1)^2 = 1
Since the the ellipse equation (2) is always 1 for each point, I can write:
(6) 4x_2^2 + (s(x_2 - x_1) + y_1)^2 = 4x_1^2 + y_1^2
(7) 4x_2^2 + s^2(x_2 - x_1)^2 + 2s(x_2 - x_1)y_1 + y_1^2 = 4x_1^2 + y_1^2
(8) 4x_2^2 + s^2(x_2 - x_1)^2 + 2s(x_2 - x_1)y_1 = 4x_1^2
(9) 4(x_2^2 - x_1^2) + s^2(x_2 - x_1)^2 + 2s(x_2 - x_1)y_1 = 0
(10) 4(x_2 - x_1)(x_2 + x_1) + s^2(x_2 - x_1)^2 + 2s(x_2 - x_1)y_1 = 0
Dividing by the term (x_2^2 - x_1^2):
(11) 4(x_2 + x_1) + s^2(x_2 - x_1) + 2s y_1 = 0
(12) 4x_2 + 4x_1 + s^2 x_2 - s^2 x_1 + 2s y_1 = 0
(13) 4x_1 - s^2 x_1 + 2s y_1 = -4x_2 - s^2 x_2
(14) 4x_1 - s^2 x_1 + 2s y_1 = x_2 (-4 - s^2)
(15) dfrac{4x_1 - s^2 x_1 + 2s y_1}{-4 - s^2} = x_2
Once I know x_2 it's a walk in the park to get y_2 with the help of (1).
Alternative Approaches
There are several approaches to this problem:
- you can use trigonometric equations instead of vector computations.
- the intersection line/ellipse often leads to a quadratic equation which I believe is more prone to rounding errors
Note
I even get the correct result when replacing double by float. That's surprising.
Interactive test
This feature is not available for the current problem.
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
#include <iostream> #include <cmath> // a simple 2D vector
struct Vector { // create new vector Vector(double x_, double y_) : x(x_), y(y_) {} double x, y; // compute length double getLength() const { return sqrt(x*x + y*y); } // dot product double dot(const Vector& other) const { return x * other.x + y * other.y; } }; // use a Vector for 2D points, too
typedef Vector Point; int main() { // count reflections unsigned int steps = 0; // initial ray Point from(0.0, 10.1); Point to (1.4, -9.6); while (true) { // exit ellipse when x is between -0.01 and +0.01 on the upper side of the ellipse if (to.x >= -0.01 && to.x <= 0.01 && to.y > 10 - 0.1) // vertical radius is 10, subtract a bit because of curving break; // find inward pointing vector of the ellipse at intersection point Vector normal(-4 * to.x, -to.y); // normalize vector length double length = normal.getLength(); normal.x /= length; normal.y /= length; // current direction of the ray Vector direction(to.x - from.x, to.y - from.y); // degenerated case ? ray will exit after only one bounce if (direction.x == 0) { steps++; // same as steps = 1 in this case break; } // reflect ray at intersection considering the normal // a short explanation can be found here: http://paulbourke.net/geometry/reflected/ Vector reflect(0, 0); reflect.x = direction.x - 2 * direction.dot(normal) * normal.x; reflect.y = direction.y - 2 * direction.dot(normal) * normal.y; // slope of the reflected ray double slope = reflect.y / reflect.x; // previous endpoint becomes the start point of the next iteration from.x = to.x; from.y = to.y; // find next intersection // I derived that strange formula in the initial comment section to.x = (4*from.x - slope*slope*from.x + 2*slope*from.y) / (-4 - slope*slope); to.y = slope * (to.x - from.x) + from.y; // count iterations steps++; } // display result std::cout << steps << std::endl; return 0; }
This solution contains 13 empty lines, 20 comments and 2 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in less than 0.01 seconds on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
June 30, 2017 submitted solution
June 30, 2017 added comments
Difficulty
Project Euler ranks this problem at 50% (out of 100%).
Links
projecteuler.net/thread=144 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
C# www.mathblog.dk/project-euler-144-investigating-multiple-reflections-of-a-laser-beam/ (written by Kristian Edlund)
C# github.com/HaochenLiu/My-Project-Euler/blob/master/144.cs (written by Haochen Liu)
Python github.com/Meng-Gen/ProjectEuler/blob/master/144.py (written by Meng-Gen Tsai)
Python github.com/smacke/project-euler/blob/master/python/144.py (written by Stephen Macke)
C++ github.com/roosephu/project-euler/blob/master/144.cpp (written by Yuping Luo)
Java github.com/thrap/project-euler/blob/master/src/Java/Problem144.java (written by Magnus Solheim Thrap)
Go github.com/frrad/project-euler/blob/master/golang/Problem144.go (written by Frederick Robinson)
Mathematica github.com/steve98654/ProjectEuler/blob/master/144.nb
Perl github.com/gustafe/projecteuler/blob/master/144-inner-reflections-in-ellipse.pl (written by Gustaf Erikson)
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 | 807 | 808 | 809 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 142 - Perfect Square Collection |

|
How many reversible numbers are there below ... - problem 145 >> |