| << problem 225 - Tribonacci non-divisors |

|
The Chase - problem 227 >> |
Problem 226: A Scoop of Blancmange
(see projecteuler.net/problem=226)
The blancmange curve is the set of points (x,y) such that 0 <= x <= 1 and y = sum_{n=0}^{infinity} dfrac{s(2^n x)}{2^n},
where s(x) is the distance from x to the nearest integer.
The area under the blancmange curve is equal to \frac12 shown in pink in the diagram below.
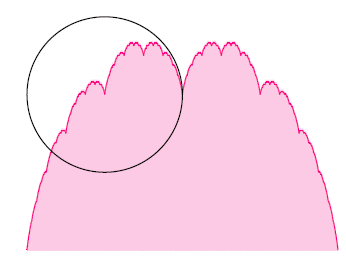
Let C be the circle with centre (\frac14, \frac12) and radius \frac14, shown in black in the diagram.
What area under the blancmange curve is enclosed by C?
Give your answer rounded to eight decimal places in the form 0.abcdefgh
My Algorithm
My idea is:
- find the left and right intersection of the circle with the blancmange curve
- numerically integrate the area between those limits
The right intersection seems to be pretty close to the centre of the blancmange.
The function
S(x) evaluates the given formula: it runs several iterations for n = 0,1,2,....The denominator grows much faster than the numerator and when a term is below my accuracy threshold
Epsilon then I stop and return the sum.If (x_b, y_b) represent a point on the blancmange curve and (x_c, y_c) a point on the circle then each intersection is a solution of
(1) d_x = | x_b - x_c | and d_y = | y_b - y_c | and radius r
(2) r^2 = d_x^2 + d_y^2
findIntersection() calls S() a lot: it slowly walks along the curve y_b = S(x_b) until it is too far from the circle.Then it turns around and walks towards the circle's center but with 50% of the previous step size.
There are four different cases to consider which make my function look ugly and I suspect this can be done a lot better.
Nevertheless, the two intersections are found pretty fast (and the right one is indeed at x = 0.5).
In order to numerically integrate the area shared by circle and blancmange curve I have to compute
(3) integral_{x_1}^{x^2} y_b - y_c
where x_1 and x_2 are the intersections (I call them
from and to in my code).Integrating the circle needs a bit of tweaking: for a circle centered at the origin I can say
(4) r^2 = x^2 + y^2
(5) y = sqrt{r^2 - x^2}
There are two solutions: the "upper" and the "lower" half of the circle. From the image it's obvious that only the lower half is of interest.
Shifting the circle to an arbitrary position changes (5) to
(6) y_c - y = sqrt{r^2 - (x_c - x)^2}
(7) y = y_c - sqrt{r^2 - (x - x_c)^2}
My program subtracts (7) from (3). I found that a step size of 0.00001 produces the correct result.
A larger step size has rounding errors while smaller step sizes are much slower.
Note
I started with incredibly small values of Epsilon and step because I suspected a heavy influence of rounding errors.
After a short debugging session I saw that much larger values still produce the correct result.
Maybe my thresholds are too tightly related to the default values of the problem such that the live test isn't correct in all cases (last digits could be "garbage").
Interactive test
You can submit your own input to my program and it will be instantly processed at my server:
This is equivalent toecho "0.2 0.4 0.25" | ./226
Output:
Note: the original problem's input 0.25 0.5 0.25 cannot be entered
because just copying results is a soft skill reserved for idiots.
(this interactive test is still under development, computations will be aborted after one second)
My code
… was written in C++11 and can be compiled with G++, Clang++, Visual C++. You can download it, too. Or just jump to my GitHub repository.
#include <iostream> #include <iomanip> #include <cmath> // smallest error threshold that still produces the correct output
const double Epsilon = 0.00000001; // compute S(x) for the blancmange curve
double S(double x) { // https://en.wikipedia.org/wiki/Blancmange_curve double result = 0; for (unsigned int n = 0; ; n++) // no abort-condition, exit when error is below epsilon threshold { auto power = pow(2, n); auto parameterS = power * x; // distance to smaller integer auto s = parameterS - floor(parameterS); // if > 0.5 then the bigger integer is closer if (s > 0.5) s = 1 - s; auto add = s / power; result += add; // enough precision ? if (add < Epsilon) return result; } } // find intersection of S and the circle by scanning x with increment step, abort if precision exceeds epsilon
double findIntersection(double circleX, double circleY, double radius, double x, double step) { while (true) { // current position on the blancmange curve auto y = S(x); // distance to the circle's center auto deltaX = x - circleX; auto deltaY = y - circleY; auto distance = sqrt(deltaX * deltaX + deltaY * deltaY); // when distance = radius, then I'm finished (allow a certain error margin Epsilon) auto error = fabs(distance - radius); if (error < Epsilon) return x; // will be true if I'm going in the wrong direction: // then turn around and decrease the step size bool turnAround = false; if (distance < radius) // keep "going away" from the circle's center { // to the right of the circle's center if (deltaX > 0 && step < 0) turnAround = true; // to the left of the circle's center if (deltaX < 0 && step > 0) turnAround = true; } else // I'm too far from the circle, need to "come back" { // to the right of the circle's center if (deltaX > 0 && step > 0) turnAround = true; // to the left of the circle's center if (deltaX < 0 && step < 0) turnAround = true; } // switch direction, smaller steps if (turnAround) step = -step / 2; // next step x += step; } } // numerically integrate area inside the circle
double integrate(double circleX, double circleY, double radius, double from, double to, double step) { double result = 0; for (auto x = from; x <= to; x += step) { auto upper = S(x); // basic circle is: r^2 = x^2 + y^2 // solved for y: y = sqrt(r^2 - x^2) // I can ignore the second solution which belongs to the "upper" part of the circle // however, the current circle isn't centered at the origin, therefore // y = circleY - sqrt(r^2 - (x - circleX)^2) auto lower = circleY - sqrt(radius*radius - (x - circleX)*(x - circleX)); // add area result += (upper - lower) * step; } return result; } int main() { auto circleX = 0.25; auto circleY = 0.5; auto radius = 0.25; std::cin >> circleX >> circleY >> radius; std::cout << std::fixed << std::setprecision(8); // find intersections auto from = findIntersection(circleX, circleY, radius, circleX, -0.1); auto to = findIntersection(circleX, circleY, radius, circleX, +0.1); // start numerical integration auto step = 0.00001; auto area = integrate(circleX, circleY, radius, from, to, step); std::cout << area << std::endl; return 0; }
This solution contains 19 empty lines, 27 comments and 3 preprocessor commands.
Benchmark
The correct solution to the original Project Euler problem was found in 0.07 seconds on an Intel® Core™ i7-2600K CPU @ 3.40GHz.
(compiled for x86_64 / Linux, GCC flags: -O3 -march=native -fno-exceptions -fno-rtti -std=gnu++11 -DORIGINAL)
See here for a comparison of all solutions.
Note: interactive tests run on a weaker (=slower) computer. Some interactive tests are compiled without -DORIGINAL.
Changelog
September 18, 2017 submitted solution
September 18, 2017 added comments
Difficulty
Project Euler ranks this problem at 65% (out of 100%).
Links
projecteuler.net/thread=226 - the best forum on the subject (note: you have to submit the correct solution first)
Code in various languages:
Python github.com/Meng-Gen/ProjectEuler/blob/master/226.py (written by Meng-Gen Tsai)
C++ github.com/roosephu/project-euler/blob/master/226.cpp (written by Yuping Luo)
C++ github.com/smacke/project-euler/blob/master/cpp/226.cpp (written by Stephen Macke)
Java github.com/thrap/project-euler/blob/master/src/Java/Problem226.java (written by Magnus Solheim Thrap)
Mathematica github.com/steve98654/ProjectEuler/blob/master/226.nb
Those links are just an unordered selection of source code I found with a semi-automatic search script on Google/Bing/GitHub/whatever.
You will probably stumble upon better solutions when searching on your own.
Maybe not all linked resources produce the correct result and/or exceed time/memory limits.
Heatmap
Please click on a problem's number to open my solution to that problem:
| green | solutions solve the original Project Euler problem and have a perfect score of 100% at Hackerrank, too | |
| yellow | solutions score less than 100% at Hackerrank (but still solve the original problem easily) | |
| gray | problems are already solved but I haven't published my solution yet | |
| blue | solutions are relevant for Project Euler only: there wasn't a Hackerrank version of it (at the time I solved it) or it differed too much | |
| orange | problems are solved but exceed the time limit of one minute or the memory limit of 256 MByte | |
| red | problems are not solved yet but I wrote a simulation to approximate the result or verified at least the given example - usually I sketched a few ideas, too | |
| black | problems are solved but access to the solution is blocked for a few days until the next problem is published | |
| [new] | the flashing problem is the one I solved most recently |
I stopped working on Project Euler problems around the time they released 617.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 |
| 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 |
| 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 |
| 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
| 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 |
| 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 |
| 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 |
| 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 |
| 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 |
| 351 | 352 | 353 | 354 | 355 | 356 | 357 | 358 | 359 | 360 | 361 | 362 | 363 | 364 | 365 | 366 | 367 | 368 | 369 | 370 | 371 | 372 | 373 | 374 | 375 |
| 376 | 377 | 378 | 379 | 380 | 381 | 382 | 383 | 384 | 385 | 386 | 387 | 388 | 389 | 390 | 391 | 392 | 393 | 394 | 395 | 396 | 397 | 398 | 399 | 400 |
| 401 | 402 | 403 | 404 | 405 | 406 | 407 | 408 | 409 | 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 | 424 | 425 |
| 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 | 438 | 439 | 440 | 441 | 442 | 443 | 444 | 445 | 446 | 447 | 448 | 449 | 450 |
| 451 | 452 | 453 | 454 | 455 | 456 | 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 | 469 | 470 | 471 | 472 | 473 | 474 | 475 |
| 476 | 477 | 478 | 479 | 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 | 493 | 494 | 495 | 496 | 497 | 498 | 499 | 500 |
| 501 | 502 | 503 | 504 | 505 | 506 | 507 | 508 | 509 | 510 | 511 | 512 | 513 | 514 | 515 | 516 | 517 | 518 | 519 | 520 | 521 | 522 | 523 | 524 | 525 |
| 526 | 527 | 528 | 529 | 530 | 531 | 532 | 533 | 534 | 535 | 536 | 537 | 538 | 539 | 540 | 541 | 542 | 543 | 544 | 545 | 546 | 547 | 548 | 549 | 550 |
| 551 | 552 | 553 | 554 | 555 | 556 | 557 | 558 | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | 569 | 570 | 571 | 572 | 573 | 574 | 575 |
| 576 | 577 | 578 | 579 | 580 | 581 | 582 | 583 | 584 | 585 | 586 | 587 | 588 | 589 | 590 | 591 | 592 | 593 | 594 | 595 | 596 | 597 | 598 | 599 | 600 |
| 601 | 602 | 603 | 604 | 605 | 606 | 607 | 608 | 609 | 610 | 611 | 612 | 613 | 614 | 615 | 616 | 617 | 618 | 619 | 620 | 621 | 622 | 623 | 624 | 625 |
| 626 | 627 | 628 | 629 | 630 | 631 | 632 | 633 | 634 | 635 | 636 | 637 | 638 | 639 | 640 | 641 | 642 | 643 | 644 | 645 | 646 | 647 | 648 | 649 | 650 |
| 651 | 652 | 653 | 654 | 655 | 656 | 657 | 658 | 659 | 660 | 661 | 662 | 663 | 664 | 665 | 666 | 667 | 668 | 669 | 670 | 671 | 672 | 673 | 674 | 675 |
| 676 | 677 | 678 | 679 | 680 | 681 | 682 | 683 | 684 | 685 | 686 | 687 | 688 | 689 | 690 | 691 | 692 | 693 | 694 | 695 | 696 | 697 | 698 | 699 | 700 |
| 701 | 702 | 703 | 704 | 705 | 706 | 707 | 708 | 709 | 710 | 711 | 712 | 713 | 714 | 715 | 716 | 717 | 718 | 719 | 720 | 721 | 722 | 723 | 724 | 725 |
| 726 | 727 | 728 | 729 | 730 | 731 | 732 | 733 | 734 | 735 | 736 | 737 | 738 | 739 | 740 | 741 | 742 | 743 | 744 | 745 | 746 | 747 | 748 | 749 | 750 |
| 751 | 752 | 753 | 754 | 755 | 756 | 757 | 758 | 759 | 760 | 761 | 762 | 763 | 764 | 765 | 766 | 767 | 768 | 769 | 770 | 771 | 772 | 773 | 774 | 775 |
| 776 | 777 | 778 | 779 | 780 | 781 | 782 | 783 | 784 | 785 | 786 | 787 | 788 | 789 | 790 | 791 | 792 | 793 | 794 | 795 | 796 | 797 | 798 | 799 | 800 |
| 801 | 802 | 803 | 804 | 805 | 806 | 807 | 808 | 809 |
I scored 13526 points (out of 15700 possible points, top rank was 17 out of ≈60000 in August 2017) at Hackerrank's Project Euler+.
My username at Project Euler is stephanbrumme while it's stbrumme at Hackerrank.
Look at my progress and performance pages to get more details.
Copyright
I hope you enjoy my code and learn something - or give me feedback how I can improve my solutions.
All of my solutions can be used for any purpose and I am in no way liable for any damages caused.
You can even remove my name and claim it's yours. But then you shall burn in hell.
The problems and most of the problems' images were created by Project Euler.
Thanks for all their endless effort !!!
| << problem 225 - Tribonacci non-divisors |

|
The Chase - problem 227 >> |